
【题目】等腰三角形ABC中,AB=CB=5,AC=8,P为AC边上一动点,PQ⊥AC,PQ与△ABC的腰交于点Q,连结CQ,设AP为x,△CPQ的面积为y,则y关于x的函数关系的图象大致是( )
A.  B.
B. 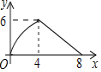 C.
C. 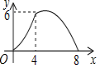 D.
D. 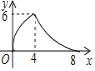
【答案】D
【解析】
过B作BD⊥AC于D,则AD=CD=4,由勾股定理可得BD=3,再分两种情况进行讨论:当Q在AB上时,求得△CPQ面积y=![]() PQ×CP=-
PQ×CP=-![]() x2+3x(0≤x<4);当Q在BC上时,求得△CPQ面积y=
x2+3x(0≤x<4);当Q在BC上时,求得△CPQ面积y=![]() PQ×CP=
PQ×CP=![]() x2-6x+24(4≤x≤8),据此判断函数图象即可.
x2-6x+24(4≤x≤8),据此判断函数图象即可.
解:过B作BD⊥AC于D,则AD=CD=4,
∴由勾股定理可得,BD=3,
如图所示,当Q在AB上时,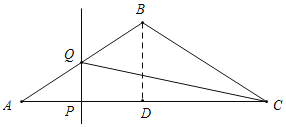
由PQ∥BD,可得![]() =
=![]() ,
,
∴PQ=![]() AP=
AP=![]() x,
x,
又∵CP=AC-AP=8-x,
∴△CPQ面积y=![]() PQ×CP=
PQ×CP=![]() ×
×![]() x×(8-x)=-
x×(8-x)=-![]() x2+3x(0≤x<4);
x2+3x(0≤x<4);
如图所示,当Q在BC上时,CP=8-x,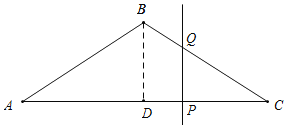
由PQ∥BD,可得PQ=![]() CP=
CP=![]() (8-x),
(8-x),
∴△CPQ面积y=![]() PQ×CP=
PQ×CP=![]() ×
×![]() (8-x)(8-x)=
(8-x)(8-x)=![]() x2-6x+24(4≤x≤8),
x2-6x+24(4≤x≤8),
∴当0≤x<4时,函数图象是开口向下的抛物线;当4≤x≤8时,函数图象是开口向上的抛物线.
故选:D.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行收费标准如下: 
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
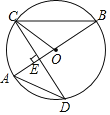
【题目】如图,AB是圆O的直径.CD是⊙O的一条弦.且CD⊥AB于点E.
(1)若∠B=32°,求∠OCE的大小;
(2)若CD=4![]() ,OE=1,求AC的长.
,OE=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
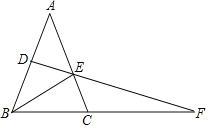
【题目】如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE
(1)求证:ED平分∠AEB;
(2)若AB=AC,∠A=38°,求∠F的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
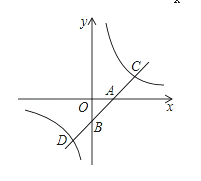
【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=![]() 于点C、D.
于点C、D.
(1)求k、b的值;
(2)写出不等式kx+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,以
,以![]() 为边在第二象限内作等边
为边在第二象限内作等边![]() .
.
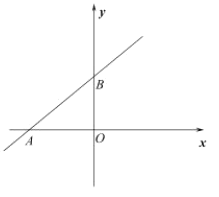
(1)求![]() 点的坐标;
点的坐标;
(2)在第二象限内有一点![]() ,使
,使![]() ,求
,求![]() 点的坐标;
点的坐标;
(3)将![]() 沿着直线
沿着直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处;再将
处;再将![]() 绕点
绕点![]() 顺时针方向旋转15°,点
顺时针方向旋转15°,点![]() 落在点
落在点![]() 处,过点
处,过点![]() 作
作![]() 轴于
轴于![]() .求
.求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
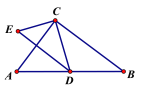
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC.
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
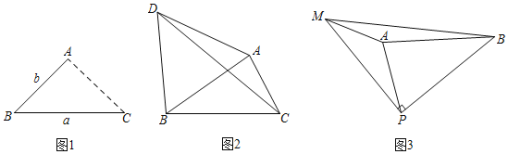
【题目】(1)发现:如图1,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]()
![]() ,当点
,当点![]() 位于 时,线段
位于 时,线段![]() 的长取得最大值,最大值为 (用含
的长取得最大值,最大值为 (用含![]() 的式子表示);
的式子表示);
(2)应用:如图2,点![]() 为线段
为线段![]() 外一动点,
外一动点,![]() ,
,![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() ,求线段
,求线段![]() 的最大值;
的最大值;
(3)拓展:如图3,线段![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 长的最大值及此时
长的最大值及此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
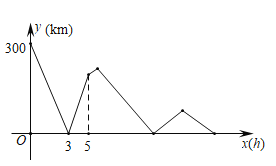
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时相向匀速行驶,当乙车到达
两地同时相向匀速行驶,当乙车到达![]() 地后,继续保持原速向远离
地后,继续保持原速向远离![]() 的方向行驶,而甲车到达
的方向行驶,而甲车到达![]() 地后,休息半小时后立即掉头,并以原速的
地后,休息半小时后立即掉头,并以原速的![]() 倍与乙车同向行驶,经过一段时间后,两车先后到达距
倍与乙车同向行驶,经过一段时间后,两车先后到达距![]() 地
地![]() 的
的![]() 地并停下来,设两车行驶的时间为
地并停下来,设两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,![]() 与
与![]() 的函数关系如图,则当甲车从
的函数关系如图,则当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地__________
地__________![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com