
【题目】已知如图,点O为△ABD的外心,点C为直径BD下方弧BCD上一点,且不与点B,D重合,∠ACB=∠ABD=45°,则下列对AC,BC,CD之间的数量关系判断正确的是( ) 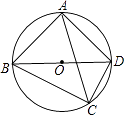
A.AC=BC+CD
B.![]() AC=BC+CD
AC=BC+CD
C.![]() AC=BC+CD
AC=BC+CD
D.2AC=BC+CD
【答案】B
【解析】解:在CD的延长线上截取DE=BC,连接EA, 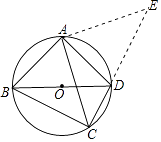
∵∠ABD=∠ACB=∠ABD=45°,
∴AB=AD,
∵∠ADE+∠ADC=180°,
∠ABC+∠ADC=180°,
∴∠ABC=∠ADE,
在△ABC与△ADE中, ,
,
∴△ABC≌△ADE(SAS),
∴∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE=90°,
∴∠ACD=∠ABD=45°,
∴△CAE是等腰直角三角形,
∴ ![]() AC=CE,
AC=CE,
∴ ![]() AC=CD+DE=CD+BC,
AC=CD+DE=CD+BC,
故选:B.
【考点精析】本题主要考查了三角形的外接圆与外心的相关知识点,需要掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,已知点P(0, ![]() ),曲线C的参数方程为
),曲线C的参数方程为 ![]() (φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ=
(φ为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ= ![]() . (Ⅰ)判断点P与直线l的位置关系并说明理由;
. (Ⅰ)判断点P与直线l的位置关系并说明理由;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )
A.![]() ﹣
﹣ ![]() =4
=4
B.![]() =4
=4
C.![]()
![]() =4
=4
D.![]()
![]() =4
=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有( )
A.9天
B.11天
C.13天
D.22天
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体健康无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加添加剂2克,B饮料每瓶需加添加剂3克,饮料加工厂生产了A、B两种饮料各多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.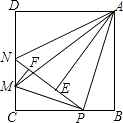
(1)发现:
△CMP和△BPA是否相似,若相似给出证明,若不相似说明理由;
(2)思考:
线段AM是否存在最小值?若存在求出这个最小值,若不存在,说明理由;
(3)探究:
当△ABP≌△ADN时,求BP的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中线重合,这样得到图②,图③,… 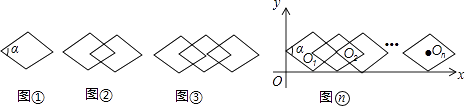
(1)观察以上图形并完成下表:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图(n)中,菱形的个数为(用含有n(n≥3)的代数式表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考前各校初三学生都要进行体育测试,某次中考体育测试设有A、B两处考点,甲、乙、丙三名学生各自随机选择其中的一处进行中考体育测试,请用表格或树状图分析:
(1)求甲、乙、丙三名学生在同一处进行体育测试的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处进行体育测试的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com