
分析 (1)首先设八年级(1)班的人均捐款数为x元,则八年级(2)班的人均捐款数为(1+20%)x元,然后根据八年级(1)班人数比八年级(2)班多8人,即可得方程:$\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=8,解此方程即可求得答案.
(2)根据(1)中的每个班级的捐款数计算各种的人数.
解答 解:(1)设八年级(1)班的人均捐款数为x元,则八年级(2)班的人均捐款数为(1+20%)x元,
则:$\frac{1200}{x}$-$\frac{1200}{(1+20%)x}$=8,
解得:x=25,
经检验,x=25是原分式方程的解.
八年级(2)班的人均捐款数为:(1+20%)x=30(元)
答:八年级(1)班人均捐款为25元,八年级(2)班人均捐款为30元.
(2)八年级(1)班的人数:$\frac{1200}{25}$=48(人).
八年级(2)班人的人数:48-8=40(人).
则总人数为:48=40=88(人).
答:这两个班的总人数是88人.
点评 本题考查分式方程的应用.注意分析题意,找到合适的等量关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
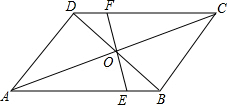 如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.
如图,在?ABCD中,EF过对角线的交点O,且与边AB、CD分别相交于点E、F、AB=4,AD=3,OF=1.3,求四边形BCFE的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
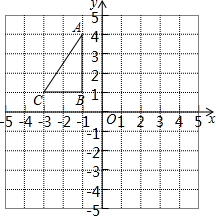 如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,Rt△ABC的三个顶点均在边长为1的正方形网格格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com