Question

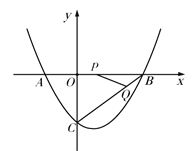
【题目】如图，在平面直角坐标系中，抛物线与轴交于、两点，与轴交于点．

（1）请直接写出A、B、C三点的坐标：

A B C

（2）点P从点A出发，在线段AB上以每秒3个单位长度的速度向点B运动，同时点Q 从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动．其中一个点到达终点时，另一个点也停止运动．设运动的时间为t(秒)，

① 当t为何值时，BP＝BQ？

② 是否存在某一时刻t，使△BPQ是直角三角形？若存在，请求出所有符合条件的t的值，若不存在，请说明理由．

Answer 1

【答案】（1）A(2，0) ，B(4，0)， C(0， )；（2）t=；（3）t=或t=

【解析】试题分析：（1）由抛物线的解析式中的y=0可求出B，A点的坐标，x=0可求出C的坐标；

(2)①分别用含t的代数式表示BP和BQ,根据BP=BQ求解即可；

②根据余弦函数，可得关于t的方程，根据解方程，可得答案．

试题解析：（1）令y=0，则，解得：x1=-2，x2=4

∴A（-2,0），B（4,0）

令x=0，则x=-3，

∴C（0，-3）

（2）①∵A（-2,0），B（4,0）

∴AB=6

BP=6-3t，BQ=t

∵BP=BQ

∴6-3t =t

解得：t=

②如图，

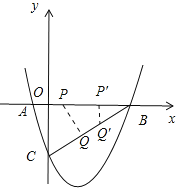
在Rt△OBC中，cos∠B=．

设运动时间为t秒，则AP=3t，BQ=t．

∴PB=6-3t．

当∠PQB=90°时，cos∠B=，即，

化简，得17t=24，解得t= ，

当∠BPQ=90°时，cos∠B=，

化简，得19t=30，解得t=，

综上所述：t=或t=时，以P，B，Q为顶点的三角形为直角三角形．