【题目】点P到x轴的距离为2，到y轴的距离为3，且在第四象限，则P点坐标是________．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，PA，PB分别与⊙O相切于点A，B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N.
（1）求证：OM = AN；
（2）若⊙O的半径R = 3，PA = 9，求OM的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】认真阅读下面的材料，完成有关问题．
材料：在学习绝对值时，老师教过我们绝对值的几何含义，如|5﹣3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5﹣（﹣3）|，所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离；|5|=|5﹣0|，所以|5|表示5在数轴上对应的点到原点的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a﹣b|．
问题（1）：点A、B、C在数轴上分别表示有理数﹣5、﹣1、3，那么A到B的距离是 ，
A到C的距离是 . （直接填最后结果）．
问题（2）：点A、B、C在数轴上分别表示有理数x、﹣2、1，那么A到B的距离与A到C的距离之和可表示为 （用含绝对值的式子表示）．
问题（3）：利用数轴探究：①找出满足|x﹣3|+|x+1|=6的x的所有值是 ；
②设|x﹣3|+|x+1|=p，当x的值取在不小于﹣1且不大于3的范围时，p的值是不变的，而且是p的最小值，这个最小值是 ；当x的值取在 的范围时，|x|+|x﹣2|的最小值是 ．
问题（4）：求|x﹣3|+|x﹣2|+|x+1|的最小值以及此时x的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】实践操作如图，∠△ABC是直角三角形，∠ACB=90，利用直尺和圆规按下列要求作图，并在图中标明相应的字母.(保留作图痕迹，不写作法)
①作∠BAC的平分线，交BC于点0
②以点0为圆心，OC为半径作圆.综合运用在你所作的图中，
(1)直线AB与⊙0的位置关系是
(2)证明:BA·BD=BC·BO;
(3)若AC=5,BC=12，求⊙0的半径
查看答案和解析>>
科目：初中数学 来源： 题型：
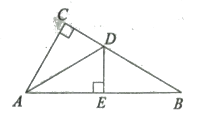
【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠CAB,交CB于点D,DE⊥AB于点E.
(1)求证：△ACD≌△AED
(2)若AC=5，△DEB的周长为8，求△ABC的周长
查看答案和解析>>
科目：初中数学 来源： 题型：
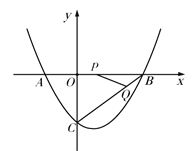
【题目】如图，在平面直角坐标系中，抛物线
与
轴交于
、
两点，与
轴交于点
．
（1）请直接写出A、B、C三点的坐标：
A B C
（2）点P从点A出发，在线段AB上以每秒3个单位长度的速度向点B运动，同时点Q 从点B出发，在线段BC上以每秒1个单位长度的速度向点C运动．其中一个点到达终点时，另一个点也停止运动．设运动的时间为t(秒)，
① 当t为何值时，BP＝BQ？
② 是否存在某一时刻t，使△BPQ是直角三角形？若存在，请求出所有符合条件的t的值，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
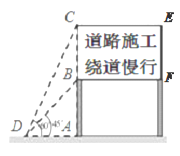
【题目】我市在高架快速公路施工期间，交管部门在施工路段设立了矩形路况警示牌BCEF（如图所示），已知立杆AB的高度是3米，从侧面D点测到路况警示牌顶端C点和底端B点的仰角分别是60°和45°，求路况警示牌宽BC的值(结果保留根号)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现定义运算：对于任意有理数a、b，都有a
b＝ab－b，如：2
3＝2×3－3，请根据以上定义解答下列各题：
（1） 2
（－3）＝___________，x
（－2）＝___________；
（2） 化简：[（－x）
3] 
（－2）；
（3） 若x
＝3
（－x），求x的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
