
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论: ①EF=BE+CF;
②∠BGC=90°+ ![]() ∠A;
∠A;
③点G到△ABC各边的距离相等;
④设GD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是 . 
【答案】①②③
【解析】解:①∵∠ABC和∠ACB的平分线相交于点G, ∴∠EBG=∠CBG,∠BCG=∠FCG.
∵EF∥BC,
∴∠CBG=∠EGB,∠BCG=∠CGF,
∴∠EBG=∠EGB,∠FCG=∠CGF,
∴BE=EG,GF=CF,
∴EF=EG+GF=BE+CF,故本小题正确;
②∵∠ABC和∠ACB的平分线相交于点G,
∴∠GBC+∠GCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A),
(180°﹣∠A),
∴∠BGC=180°﹣(∠GBC+∠GCB)=180°﹣ ![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+ ![]() ∠A,故本小题正确;
∠A,故本小题正确;
③∵∠ABC和∠ACB的平分线相交于点G,
∴点G是△ABC的内心,
∴点G到△ABC各边的距离相等,故本小题正确;
④连接AG,
∵点G是△ABC的内心,GD=m,AE+AF=n,
∴S△AEF= ![]() AEGD+
AEGD+ ![]() AFGD=
AFGD= ![]() (AE+AF)GD=
(AE+AF)GD= ![]() nm,故本小题错误.
nm,故本小题错误.
所以答案是:①②③.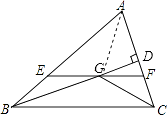
【考点精析】关于本题考查的平行线的性质和角平分线的性质定理,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC.D为BC上一点,且到A,B两点的距离相等. 
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连接AD,若∠B=35°,求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com