
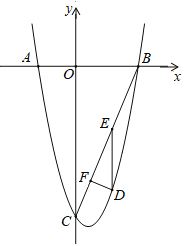
����Ŀ����ͼ�����κ���y��ax2+bx��12��ͼ��x����A����3��0����B��5��0�����㣬��y�ύ�ڵ�C����D���������ϵ�һ�����㣮
��1���������ߵĽ���ʽ��
��2�����D�ĺ�����Ϊm�����ҵ�m��x��m+5ʱ����Ӧ�ĺ���ֵy���㩁![]() m����m��ֵ��
m����m��ֵ��
��3������D�ڵ��������ڣ�����D��DE��y�ύBC��E��DF��BC��F���߶�EF�ij����Ƿ�������ֵ�������ڣ������������ֵ����Ӧ��D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��![]() x2��
x2��![]() x��12����2��m��ֵΪ��
x��12����2��m��ֵΪ��![]() ��0����3����D����Ϊ��
��0����3����D����Ϊ��![]() ����11��ʱ���߶�EF���ȵ����ֵΪ
����11��ʱ���߶�EF���ȵ����ֵΪ![]() ��
��
��������
��1����֪�����߹���A��B���ô���ϵ���������������ʽ��
��2���Ѷ��κ����䷽��ö���Ϊ��1����![]() ������x��1ʱ�����κ�������Сֵy����
������x��1ʱ�����κ�������Сֵy����![]() ������m��x��m+5��Χ������ֵy��Ӧ����СֵҲΪ��
������m��x��m+5��Χ������ֵy��Ӧ����СֵҲΪ��![]() ����x��1��m��x��m+5�ķ�Χ�ڣ���m��1��m+5����é�4��m��1����Ϊ��ȷ��x��m����x��m+5ʱȡ����Ӧ�����ֵ������������ۣ���x��m��Գ����Զ����x��mʱȡ�����ֵ��
����x��1��m��x��m+5�ķ�Χ�ڣ���m��1��m+5����é�4��m��1����Ϊ��ȷ��x��m����x��m+5ʱȡ����Ӧ�����ֵ������������ۣ���x��m��Գ����Զ����x��mʱȡ�����ֵ��![]() m��������㼴���m��ֵ����x��m+5��Գ�������Զ����x��m+5ʱȡ�����ֵ��������㼴���m��ֵ��
m��������㼴���m��ֵ����x��m+5��Գ�������Զ����x��m+5ʱȡ�����ֵ��������㼴���m��ֵ��
��3����DE��y��ɵá�DEF����BCO����D���E��������ͬ�����D������Ϊd����d��ʾ��D�����꣮���ֱ��BC����ʽ������d��ʾ��E���꣬��������d��ʾDE�ij��ȣ�����DF��BC��E������cos��DEF��![]() ����Rt��BOC������cos��BCO��ֵ���ɡ�DEF����BCO��cos��DEF��cos��BCO�����ú�d�Ķ���ʽ��ʾEF���䷽�����EF�����ֵ��
����Rt��BOC������cos��BCO��ֵ���ɡ�DEF����BCO��cos��DEF��cos��BCO�����ú�d�Ķ���ʽ��ʾEF���䷽�����EF�����ֵ��
�⣺��1���߶��κ���y��ax2+bx��12��ͼ�����A����3��0����B��5��0��
��![]() ��ã�
��ã�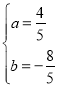 ,
,
�������ߵĽ���ʽΪy��![]() x2��
x2��![]() x��12
x��12
��2����y��![]() x2��
x2��![]() x��
x��![]() ��x��1��2��
��x��1��2��![]()
�൱x��1ʱ�����κ�������Сֵy����![]()
�ߵ�m��x��m+5ʱ����Ӧ�ĺ���ֵy���㩁![]() ��y��
��y��![]() m
m
��Գ��x��1��m��x��m+5�ķ�Χ�ڣ���m��1��m+5
����4��m��1
ȡ�㣨m��0����㣨m+5��0�����е�M��m+![]() ��
��
�ٵ�m+![]() ��1ʱ������4��m����
��1ʱ������4��m����![]() ����M�ڶԳ������
����M�ڶԳ������
��x��m���Գ���ľ����x��m+5���Գ���ľ���Զ
��x��mʱ��yȡ�����ֵ
��![]() m2��
m2��![]() m��12����
m��12����![]() m
m
��ã�m1��![]() ����ȥ����m2����
����ȥ����m2����![]()
�ڵ�m+![]() ��1ʱ������
��1ʱ������![]() ��m��1����M�ڶԳ����Ҳ�
��m��1����M�ڶԳ����Ҳ�
��x��m+5���Գ���ľ����x��m���Գ���ľ���Զ
��x��m+5ʱ��yȡ�����ֵ
��![]() ��m+5��2��
��m+5��2��![]() ��m+5����12����
��m+5����12����![]() m
m
��ã�m1����10����ȥ����m2��0
����������m��ֵΪ��![]() ��0��
��0��
��3���ߵ�x��0ʱ��y��![]() x2��
x2��![]() x��12����12
x��12����12
��C��0����12��
��B��5��0������BOC��90��
��ֱ��BC��y��![]() x��12��BC��
x��12��BC��![]()
��Rt��BOC��cos��BCO��![]()
��DE��y��
���DEF����BCO��xE��xD
��D��d��![]() d2��
d2��![]() d��12����0��d��5������E��d��
d��12����0��d��5������E��d��![]() d��12��
d��12��
��DE��![]() d��12����
d��12����![]() d2��
d2��![]() d��12������
d��12������![]() d2+4d����
d2+4d����![]() ��d��
��d��![]() ��2+5
��2+5
��DF��BC
���DFE��90��
��cos��DEF��![]() ��cos��BCO��
��cos��BCO��![]()
��EF��![]() DE����
DE����![]() ��d��
��d��![]() ��2+
��2+![]()
�൱d��![]() ʱ��EF���ֵΪ
ʱ��EF���ֵΪ![]()
��ʱ��yD��![]() ����
����![]() ��2��
��2��![]() ��
��![]() ��12����11
��12����11
���D����Ϊ��![]() ����11��ʱ���߶�EF���ȵ����ֵΪ
����11��ʱ���߶�EF���ȵ����ֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������߹�·�����ȣ���ز����ⶨ��һ�����̶Ӷ�39000�Ĺ�·����·�桰�ĺڡ����̣��ù��̶Ӽƻ�ʹ��һ��һС�����ͺ��豸����ķ�ʽʩ����ԭ�ƻ�С���豸ÿСʱ����·��30�ף������豸ÿСʱ����·��60��
��1������С���豸����Ч�ʽϵͣ��ù��̶Ӽƻ�ʹ�ô����豸��ʱ���ʹ��С���豸��ʱ���![]() ������������깤ʱ��С���豸��ʹ��ʱ������Ϊ����Сʱ��
������������깤ʱ��С���豸��ʹ��ʱ������Ϊ����Сʱ��
��2��ͨ�����졢�������˲���֧�߹�·����������˹��̵�ʵ��ʩ����̱�����ⶨ���������39000����9000�ף�������ʵ��ʩ���У�С���豸�����蹫·Ч�ʲ��������£�ʹ��ʱ��ȣ�1���е���Сֵ��![]() ��ͬʱ����Ϊ���˲��������豸����������ʹ�ô����豸���蹫·��Ч�ʱ�ԭ�ƻ��½���
��ͬʱ����Ϊ���˲��������豸����������ʹ�ô����豸���蹫·��Ч�ʱ�ԭ�ƻ��½���![]() ��ʹ��ʱ��ȣ�1���д����豸ʹ�õ����ʱ���
��ʹ��ʱ��ȣ�1���д����豸ʹ�õ����ʱ���![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ��������й�ʫ�ʴ��������ѡ�κ���![]() ��ѧ���μӾ�������
��ѧ���μӾ�������![]() ��ѧ��ͬʱĬд
��ѧ��ͬʱĬд![]() ��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�
��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�![]() �֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ����:
�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ����:
��� | �ɼ� | Ƶ��(����) |
�� |
|
|
�� |
|
|
�� |
|
|
�� |
|
|
�� |
|
|
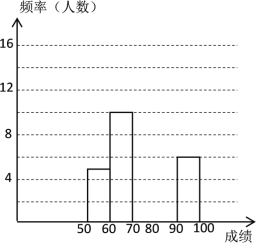
����ͼ��������и���: :
��1���������![]() ��ֵ;
��ֵ;
��Ƶ���ֲ�ֱ��ͼ��������;
��2�������Գɼ�������![]() ��Ϊ���㣬�β��Ե��������Ƕ���?
��Ϊ���㣬�β��Ե��������Ƕ���?
��3����![]() ��
��![]() ��ͬѧ�У���
��ͬѧ�У���![]() ����ͬѧ���ֽ���
����ͬѧ���ֽ���![]() ��ͬѧƽ���ֳ�������жԿ�������
��ͬѧƽ���ֳ�������жԿ�������![]() ����ͬѧÿ������ˣ�������С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
����ͬѧÿ������ˣ�������С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
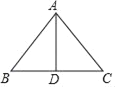
����Ŀ����ͼ���ڵ���������ֽƬABC�У�AB=AC=10��BC=12�����˵���������ֽƬ�صױ�BC�ϵĸ�AD��������ȫ�ȵ������Σ���������������ƴ��һ��ƽ���ı��Σ�����ƴ��������ƽ���ı�������ĶԽ��ߵij���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��������������A��B����ͬһˮƽ�����ϡ�һ�����˻��ڿ�����MN����ˮƽ���н��к�����ҵ��MN��AB��ͬһǦֱƽ���ڣ������˻�������C��ʱ����þ���A�ĸ���Ϊ45��������B�ĸ���Ϊ30������ʱC������ľ���CDΪ100�ף���������A��B��ľ���Ϊ__�ף�����������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
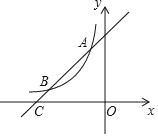
����Ŀ����ͼ��һ�κ���y��x+4��ͼ���뷴��������y��![]() (kΪ������k��0)��ͼ����A(��1��a)��B���㣬��x�ύ�ڵ�C��
(kΪ������k��0)��ͼ����A(��1��a)��B���㣬��x�ύ�ڵ�C��
(1)��a��k��ֵ����B�����ꣻ
(2)����P��x���ϣ���S��ACP��![]() S��BOC��ֱ��д����P�����꣮
S��BOC��ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() .������
.������![]() ��һԪ���η���
��һԪ���η���![]() ��
��![]() �ķ�Χ����ʵ��������
�ķ�Χ����ʵ��������![]() ��ȡֵ��Χ��_____________.
��ȡֵ��Χ��_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
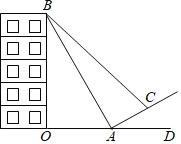
����Ŀ��ijУ��ѧ����ʵ��С��һ�λ�У�����һ��¥���ĸ߶ȣ���ͼ����ɽ���½�A���������¥����¥��B�������Ϊ60�㣬��ɽ�������ߵ�C���ٲ��B�������Ϊ45�㣬��֪ɽ�µ��±�i��1��![]() ��OA��200m����O��A��D��ͬһ��ֱ���ϣ�
��OA��200m����O��A��D��ͬһ��ֱ���ϣ�
(1)��¥��OB�ĸ߶ȣ�
(2)��ɽ����AC�ľ���(�����������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCD�ڽ���ԲO��AC��ԲO��ֱ��������A��������CD���ӳ����ཻ�ڵ�P.�ҡ�APC����BCP.
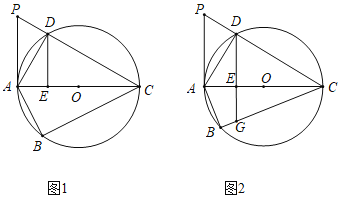
(1)��֤����BAC��2��ACD.
(2)��ͼ1�еĵ�D��DE��AC��E����BC��G(��ͼ2)��BG��GE��3��5��OE��5�����O�İ뾶.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com