Question

如图，半径为2的⊙E交x轴于A、B，交y轴于点C、D，直线CF交x轴负半轴于点F，连接EB、EC．已知点E的坐标为(1，1)，∠OFC＝30°．

(1)求证：直线CF是⊙E的切线；(2)求证：AB＝CD；(3)求图中阴影部分的面积．

 

Answer 1

（1）证明见解析；（2）证明见解析；（3）阴影部分的面积为（）．

【解析】

试题分析：（1）首先过点E作EG⊥y轴于点G，由点E的坐标为（1，1），可得EG=1．继而可求得∠ECG的度数，又由∠OFC=30°，∠FOC=90°，可求得∠FCE=∠OCF+∠ECG=90°．

（2）首先过点E作EH⊥x轴于点H，易证得Rt△CEG≌Rt△BEH，又由EH⊥AB，EG⊥CD，则可证得AB=CD；

（3）连接OE，可求得OC=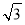+1与∠OEB+∠OEC=210°，继而可求得阴影部分的面积．

试题解析：（1）过点E作EG⊥y轴于点G，

∵点E的坐标为（1，1），

∴EG=1．

在Rt△CEG中，sin∠ECG=，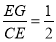

∴∠ECG=30°．

∵∠OFC=30°，∠FOC=90°，

∴∠OCF=180°﹣∠FOC﹣∠OFC=60°．

∴∠FCE=∠OCF+∠ECG=90°．

即CF⊥CE．

∴直线CF是⊙E的切线；

（2）过点E作EH⊥x轴于点H，

∵点E的坐标为（1，1），

∴EG=EH=1．

在Rt△CEG与Rt△BEH中，

∵，

∴Rt△CEG≌Rt△BEH（HL）．

∴CG=BH．

∵EH⊥AB，EG⊥CD，

∴AB=2BH，CD=2CG．

∴AB=CD；

（3）连接OE，

在Rt△CEG中，CG=，

∴OC=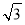+1．

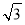同理：OB=+1．

∵OG=EG，∠OGE=90°，

∴∠EOG=∠OEG=45°．

又∵∠OCE=30°，

∴∠OEC=180°﹣∠EOG﹣∠OCE=105°．

同理：∠OEB=105°．

∴∠OEB+∠OEC=210°．

∴S阴影=．

考点：圆的综合题．