
����Ŀ����ͼ1����֪������y1��x2+mx��������y2��ax2+bx+c����״��ͬ�����ڷ����෴�����ཻ�ڵ�A����3����6���͵�B��1��6����������y2��x�������ύ�ڵ�C��PΪ������y2��A��B�����һ���㣬����P��PQ��y�ᣬ��y1���ڵ�Q��
��1����������y1��������y2�Ľ���ʽ��
��2���ı���APBO�����ΪS����S�����ֵ����д����ʱ��P�����ꣻ
��3����ͼ2��y2�ĶԳ���Ϊֱ��l��PC��l���ڵ�E���ڣ�2���������£�ֱ��l���Ƿ����һ��T��ʹ����T��E��CΪ���������������APQ���ƣ�������ڣ������T�����ꣻ��������ڣ�˵�����ɣ�

���𰸡���1��y2����x2+x+6����2����t����1ʱ��S�����16����ʱP������Ϊ����1��4������3�����ڵ�T������![]() ��
��![]() ʹ��T��C��EΪ��������������PAQ���ƣ�
ʹ��T��C��EΪ��������������PAQ���ƣ�
��������
��1���ֱ����ô���ϵ�������������κ����Ľ���ʽ��
��2�����P������Ϊt����P��t����t2+t+6����Q��t��t2+5t������ʾPQ�ij�������������������Ϳɵ�S��t�Ĺ�ϵʽ���䷽��ɵ�S�����ֵ��
��3����ȷ����AQB��135�������Է�������ۿɵý��ۣ�
�⣺��1����B��1��6������y1��x2+mx�ã�m��5��
��y1��x2+5x��
��y2��y1��״��ͬ�������෴��
��a����1��
��y2����x2+bx+c��
��A����3����6����B��1��6������ã�
![]() ��
��
��ã�b��1��c��6��
��y2����x2+x+6��
��2�����P������Ϊt��
��P��t����t2+t+6����Q��t��t2+5t����
��PQ����t2+t+6��t2��5t����2t2��4t+6��
��S�ı���APBQ��![]()
����4��t+1��2+16��
�൱t����1ʱ��S�����16����ʱP������Ϊ����1��4����
��3�����ڵ�T��
��y2����x2+x+6����ֱ��lΪ��x��![]() ��
��
�ɣ�2��֪P�������Ϊ����1��4����
��x����1ʱ��y1������1��2+5������1������4��
��Q�����������1����4����
��A����3����6����
�x2+x+6��0�ã�CΪ��3��0����
��ͼ2����PQ��x�ύ�ڵ�G��ֱ��l��x�ύ�ڵ�M��

��AH��PQ���ӳ��ߣ�����Ϊ��H����֪AH��2��HQ����4������6����2��
���AQH��45����
���AQP��180����45����135����
��PG��4��CG��3+1��4��
���ECO��45����
��T����E���Ϸ���CET��135��
MC��3��![]() ��
��![]() ��EC��
��EC��![]() MC��
MC��![]() ��
��
AQ��![]() AH��2
AH��2![]() ��PQ��8��
��PQ��8��
�������������
������PAQ�ס�TCE����![]() ��
��
��TE��![]() ��10����ʱT������Ϊ
��10����ʱT������Ϊ![]() ��
��
������PAQ�ס�CTE����![]() ��
��
��TE��![]() ����ʱT������Ϊ
����ʱT������Ϊ![]() ,
,
���Ͽ�֪���ڵ�T������![]() ��
��![]() ʹ��T��C��EΪ���������������PAQ���ƣ�
ʹ��T��C��EΪ���������������PAQ���ƣ�


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����-1,1, 2�����������У������ȡһ��������Ϊ��.��ô��ʹ����x��һ�κ���![]() ��ͼ����x�ᡢy��Χ�ɵ����������Ϊ
��ͼ����x�ᡢy��Χ�ɵ����������Ϊ![]() ����ʹ����x�IJ���ʽ��
����ʹ����x�IJ���ʽ��![]() �н�ĸ���Ϊ .
�н�ĸ���Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ����ͯ�ڣ�ij��߳���������һ����ͼ��ʾ�Ŀ�������ת����ת�̣���չ�н��������˿�����߾��ܻ��һ��ת��ת�̵Ļ��ᣬ��ת��ֹͣʱ��ָ��������һ����Ϳ��Ի����Ӧ��Ʒ���±��Ǹû��һ��ͳ�����ݣ�����˵�����ٵ�n�ܴ�ʱ������ָ��������Ǧ���������Ƶ�ʴ�Լ��0.70���ڼ�����ȥת��ת��һ�Σ����Ǧ�ʵĸ��ʴ�Լ��0.70�������ת��ת��2000�Σ�ָ���������ľߺ�������Ĵ�����Լ��600�Σ���ת��ת��10�Σ�һ����3�λ���ľߺ�.����ȷ����_____
ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
������Ǧ��������Ĵ���m | 68 | 108 | 140 | 355 | 560 | 690 |
������Ǧ���������Ƶ�� | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ���ӳ��ֱ�
���ӳ��ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() .
.
��1����![]() �ij�.
�ij�.
��2������![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ��ֵ.
��ֵ.
��3�����ʵ�![]() �ij�����ʲô����ʱ�����߶�
�ij�����ʲô����ʱ�����߶�![]() ��ǡ��ֻ��һ��
��ǡ��ֻ��һ��![]() ��ʹ��
��ʹ��![]() ?
?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
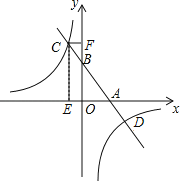
����Ŀ����ͼ����֪һ�κ���y��kx+b��ͼ����x�ᣬy��ֱ��ཻ��A��B���㣬���뷴��������y��![]() ���ڵ�C��D����CE��x�ᣬ����ΪE��CF��y�ᣬ����ΪF����BΪOF���е㣬�ı���OECF�����Ϊ16����D������Ϊ��4����b����
���ڵ�C��D����CE��x�ᣬ����ΪE��CF��y�ᣬ����ΪF����BΪOF���е㣬�ı���OECF�����Ϊ16����D������Ϊ��4����b����
��1����һ�κ�������ʽ�ͷ�������������ʽ��
��2�������C���꣬������ͼ��ֱ��д������ʽkx+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
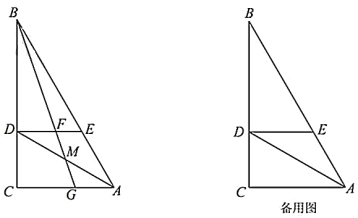
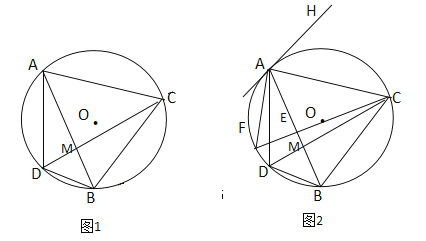
����Ŀ����ͼ1����֪��O����ADB�����Բ����ADB��ƽ����DC��AB�ڵ�M������O�ڵ�C������AC��BC.
��1����֤��AC=BC��
��2����ͼ2����ͼ1 �Ļ���������O��ֱ��CF��AB�ڵ�E������AF������A����O������AH����AH//BC�����ACF�Ķ�����
��3���ڣ�2���������£�����ABD�����Ϊ![]() ����ABD����ABC�������Ϊ2��9����CD�ij�.
����ABD����ABC�������Ϊ2��9����CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�������½ǵĶ��㰴˳ʱ�뷽����ת90����ͼ��λ�ã����������½ǵĶ��㰴˳ʱ�뷽����ת90����ͼ��λ�ã��Դ����ƣ�����������ת2017�Σ���AB=4��AD=3����A��������ת��������������·���ܳ�Ϊ�� ��

A. 2017�� B. 2034�� C. 3024�� D. 3026��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b��˫����![]() ��x��0���ཻ��A��-4��a����B��-1��4������.
��x��0���ཻ��A��-4��a����B��-1��4������.

��1����ֱ�ߺ�˫���ߵĽ���ʽ��
��2����y���ϴ���һ��P��ʹ��PA+PB��ֵ��С�����P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
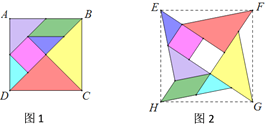
����Ŀ�����ɰ����������ȵ�һ��Խ���죬����������Ϊ������ħ���������������ͼ�����Σ���ͼ1�������糵��������ͼ2��������ͬһ�����ɰ�ƴ�ɵģ���ͼ��������ABCD��EFGH�������Ϊ______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com