Question

2．在⊙O中，OC⊥弦AB，垂足为C，点D在⊙O上．
（1）如图1，已知OA=5，AB=6，如果OD∥AB，CD与半径OB相交于点E，求DE的长；
（2）已知OA=5，AB=6（如图2），如果射线OD与AB的延长线相交于点F，且△OCD是等腰三角形，求AF的长；
（3）如果OD∥AB，CD⊥OB，垂足为E，求sin∠ODC的值．

Answer 1

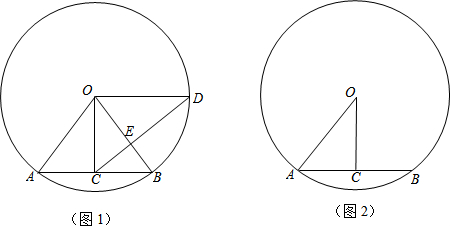
分析 （1）由在⊙O中，OC⊥弦AB，可求得AC与OC的长，又由OD∥AB，可得OD⊥OC，即可求得CD的长，然后由相似三角形的对应边成比例，求得答案；
（2）由△OCD是等腰三角形，OD＞OC，可分别从当DC=OD=5时与当DC=OC=4时，去分析求解即可求得答案；
（3）首先设OB=OD=r，BC=x，即可表示出OC，易得∠COB=90°-∠DOE=∠ODC，即可得tan∠COB=tan∠ODC，可得$\frac{x}{{\sqrt{{r^2}-{x^2}}}}=\frac{{\sqrt{{r^2}-{x^2}}}}{r}$，继而求得答案．

解答 解：（1）∵在⊙O中，OC⊥AB，
∴AC=$\frac{1}{2}AB=3$，OC=$\sqrt{A{O^2}-A{C^2}}$=4，
∵OD∥AB，
∴OD⊥OC，△ODE∽△BCE，
∴CD=$\sqrt{O{C^2}+O{D^2}}=\sqrt{{4^2}+{5^2}}=\sqrt{41}$．
∵$\frac{DE}{CE}=\frac{OD}{BC}=\frac{5}{3}$，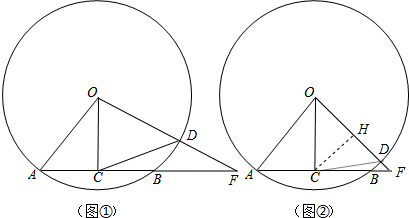
∴$\frac{DE}{CD}=\frac{5}{8}$，
∴DE=$\frac{5}{8}\sqrt{41}$；

（2）∵△OCD是等腰三角形，OD＞OC，
∴如图①，当DC=OD=5时，∠DOC=∠DCO，
∵∠DFC+∠DOC=∠DCF+∠DCO=90°，
∴∠DFC=∠DCF，
∴DF=DC=DO=5，OF=10，
∴CF=$\sqrt{O{F^2}-O{C^2}}=\sqrt{{{10}^2}-{4^2}}=2\sqrt{21}$，$AF=3+2\sqrt{21}$；
如图②，当DC=OC=4时，作△DOC的高CH，
∴$OH=\frac{1}{2}OD=\frac{5}{2}$，CH=$\sqrt{O{C^2}-O{H^2}}=\sqrt{{4^2}-{{（\frac{5}{2}）}^2}}=\frac{1}{2}\sqrt{39}$；
∴tan∠FOC=$\frac{CF}{OC}=\frac{CH}{OH}=\frac{{\sqrt{39}}}{5}$，
∴$CF=\frac{{4\sqrt{39}}}{5}$．$AF=3+\frac{{4\sqrt{39}}}{5}$；

（3）设OB=OD=r，BC=x，则$OC=\sqrt{O{B^2}-B{C^2}}=\sqrt{{r^2}-{x^2}}$，
∵OD∥AB，OC⊥AB，
∴OD⊥OC，
又∵CD⊥OB，
∴∠COB=90°-∠DOE=∠ODC，
∴tan∠COB=tan∠ODC，
∴$\frac{BC}{OC}=\frac{OC}{OD}$，
∴$\frac{x}{{\sqrt{{r^2}-{x^2}}}}=\frac{{\sqrt{{r^2}-{x^2}}}}{r}$，
∴xr=r²-x²，x²+rx-r²-0，
∵r≠0，${（\frac{x}{r}）^2}+\frac{x}{r}-1≠0$，$\frac{x}{r}=\frac{{-1±\sqrt{5}}}{2}$（负值舍去），
∴sin∠ODC=sin∠COB=$\frac{BC}{OB}=\frac{x}{r}=\frac{{\sqrt{5}-1}}{2}$．

点评 此题属于圆的综合题，考查了相似三角形的判定与性质、勾股定理、等腰三角形的性质以及三角函数的性质．注意分类讨论思想的应用，注意掌握辅助线的作法．