
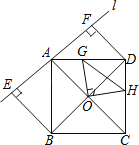
【题目】如图直线l经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BE⊥l于点E,DF⊥l于点F.以正方形对角线的交点O为端点,引两条相互垂直的射线分别与AD、CD交于G、H两点,若EF=2,S△ABE=![]() ,则线段GH长度的最小值是____.
,则线段GH长度的最小值是____.
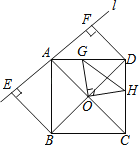
【答案】1.
【解析】
∵直线l经过正方形ABCD的顶点A,BE⊥l于点E,DF⊥l于点F.
∴∠BAD=∠BDA=∠DFA=90°,AB=AD.
∴∠ABE+∠BAE=90°,∠DAF+∠BAE=90°,
∴∠ABE=∠DAF,
∴△ABE≌△DAF,
∴BE=AF.
设AE=![]() ,则由EF=2,可得:AF=
,则由EF=2,可得:AF=![]() =BE,
=BE,
又∵S△ABE=![]() ,
,
∴![]() ,解得:
,解得:![]() ,即AE=1,
,即AE=1,
∴BE=AF=EF-AE=2-1=1.
∴AB=![]() =AD=CD.
=AD=CD.
∵四边形ABCD是正方形,OG⊥OH,
∴∠AOD=∠GOH=90°,OA=OD,∠OAG=∠ODH=45°,
∴∠AOG+∠GOD=90°,∠GOD+∠DOH=90°,
∴∠AOG=∠DOH,
∴△AOG≌△DOH,
∴OG=OH.
∴GH=![]() .
.
∴当OG最小时,GH最小.
∵当OG⊥AD时,OG最小,而此时由OA=OD,∠AOD=90°可得OG=![]() AD=
AD=![]() ,
,
∴GH最小=![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
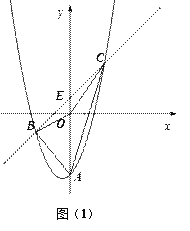
【题目】如图(1),抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C .
与抛物线交于点B、C .
(1)则点A的坐标是 ______ ;
(2)当b = 0时(如图(2)),△ABE与△ACE的面积大小关系如何?当![]() 时,上述关系还成立吗,为什么?
时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC 为斜边的直角三角形,若存在,求出b;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)(
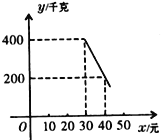
(元)(![]() )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得 最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=![]() BC,③OD=
BC,③OD=![]() BF,④∠CHF=45°。正确结论的个数为( )
BF,④∠CHF=45°。正确结论的个数为( )
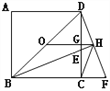
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
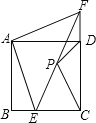
【题目】如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(1)求证:AE=AF;
(2)若∠AEB=75°,求∠CPD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O和⊙O上的一点A(如图).
(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题的作图中,如果点E在![]() 上,求证:DE是⊙O内接正十二边形的边.
上,求证:DE是⊙O内接正十二边形的边.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有4个质地、大小均相同的小球,这些小球上分别标有数字3、4、5、x.甲、乙两人每次从袋中各随机摸出1球,并计算摸出这2个小球上数字之和,记录后都将放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出现频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出现频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”频率将稳定在它概率附近.估计
出现“和为8”概率是________.
0.33
(2)如果摸出的这两个小球上数字之和为9概是![]() ,那么x值可以取7吗?请用列表法或画树状图法说明理由;如果x值不可以取7,请写出一个符合要求x值.
,那么x值可以取7吗?请用列表法或画树状图法说明理由;如果x值不可以取7,请写出一个符合要求x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AD=4,AB=3,如果点E在边BC上,将纸片沿AE折叠,使点B落在点F处,联结FC,当△EFC是直角三角形时,那么BE的长为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com