
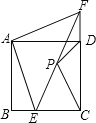
【题目】如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(1)求证:AE=AF;
(2)若∠AEB=75°,求∠CPD的度数.
【答案】(1)证明见解析;(2)105°.
【解析】
试题
(1)由已知条件证△ABE≌△ADF即可可得到AE=AF;
(2)
试题解析:
(1)∵四边形ABCD为正方形,
∴∠B=∠ADC=∠ADF=90°,AB=AD,
又∵BE=DF,
∵在△ABE和△ADF中,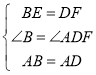 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF;
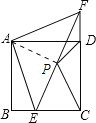
(2)连结AP,
∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAD=90°,即∠EAF=90°,
又∵AE=AF,
∴∠AEF=45°,
∵∠AEB=75°,
∴∠CEF=180°﹣45°﹣75°=60°,
∴∠EFC=180°-90°-60°=30°,
∵∠ECF=90°,P为EF中点,
∴CP=PF=![]() EF,
EF,
∴∠EFC=∠PCF=30°,
∵P为EF中点,∠EAF=90°,
∴AP=![]() EF,
EF,
∴AP=CP,
∵在△APD和△CPD中: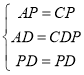 ,
,
∴△APD≌△CPD(SSS),
∴∠ADP=∠CDP=![]() ∠ADC=45°,
∠ADC=45°,
∴∠CPD=180°﹣∠PCD﹣∠CDP=105°.


科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图,图象过点(﹣1,0),对称轴为直线
的部分图象如图,图象过点(﹣1,0),对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时, ![]() 随
随![]() 的增大而增大.其中正确的结论有( )
的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
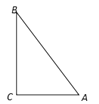
【题目】新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在RtΔABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为 ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小华身高1.78米,他乘电梯会有碰头危险吗?姚明身高2.26米,他乘电梯会有碰头危险吗?(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)

查看答案和解析>>
科目:初中数学 来源: 题型:
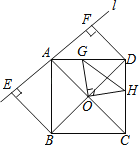
【题目】如图直线l经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BE⊥l于点E,DF⊥l于点F.以正方形对角线的交点O为端点,引两条相互垂直的射线分别与AD、CD交于G、H两点,若EF=2,S△ABE=![]() ,则线段GH长度的最小值是____.
,则线段GH长度的最小值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com