Question

【题目】如图1，抛物线与x轴交于A(1,0)，B(4，0)，与y轴交于点C.

(1)求抛物线的解析式;

(2)抛物线上一点D,满足，求点D的坐标;

(3)如图2，已知N（0,1），将抛物线在点A、B之间部分（含点A、B）沿轴向上翻折，得到图象T（虚线部分），点M为图象T的顶点，现将图象T保持其顶点在直线MN上平移，得到的图象T1与线段BC至少有一个交点，求图象T1的顶点横坐标的取值范围.

Answer 1

【答案】（1）y=x2-5x+4;(2) D（;(3)

【解析】试题分析：(1)待定系数法解抛物线的解析式；

（2）分两种情况讨论：当D在直线AC的左侧时和当D在直线AC的右侧时，求得点D的坐标；

（3）两种极值情况求得m的值,两值之间范围即符合题意

试题解析：

（1）将A(1,0)，B(4，0)代入抛物线的解析式得：

解得：b=-5，c=4

∴抛物线的解析式为：

（2）∵A（1,0），C（0,4）

∴直线AC的解析式为

当D在直线AC的左侧时，∵

∴OD∥AC

∴直线OD的解析式为

∴

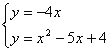
方程组无解，

∴D不在直线AC的左侧

当D在直线AC的右侧时，在x轴上取点M（2,0），则，

过点M作直线DM∥AC交抛物线于点D，则直线DM的解析式为，

∴

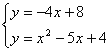
解得，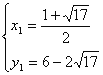

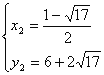
∴D（，）或（，）

（3）解：设抛物线：的顶点为G，则点G(2.5，-2.25)关于x轴

对称点M的坐标为：M(2.5，2.25)，

又∵N（0，1）解得直线MN：,

∵图象T顶点在直线MN上,

∴设图象T1顶点为

如图，由点A（1，0）与M(2.5，2.25)的坐标关系，得到点A的对应点,即又BC：

当点K在BC上时,,

∴

∴,

∵，

∴点K在线段BC上,

设图象T1所在抛物线方程为：，点L为直线BC与抛物线的交点，则点L的坐标满足下列方程组：

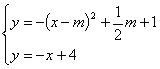
点L的横坐标是方程：的解

当图象T1与直线BC相切时有：

=0

∴

∴,

∵,

∴点L在图象T1上

∵，

∴点L在线段BC上

∴图象T1顶点横坐标的取值范围：.