
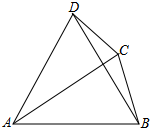
 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )| A. | 18° | B. | 20° | C. | 25° | D. | 15° |
分析 延长BD到M使得DM=DC,由△ADM≌△ADC,得AM=AC=AB,得△AMB是等边三角形,得∠ACD=∠M=60°,再求出∠BAC即可解决问题.
解答 解:如图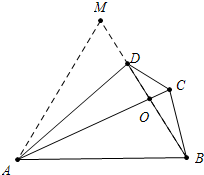 延长BD到M使得DM=DC,
延长BD到M使得DM=DC,
∵∠ADB=78°,
∴∠ADM=180°-∠ADB=102°,
∵∠ADB=78°,∠BDC=24°,
∴∠ADC=∠ADB+∠BDC=102°,
∴∠ADM=∠ADC,
在△ADM和△ADC中,
$\left\{\begin{array}{l}{AD=AD}\\{∠ADM=∠ADC}\\{DM=DC}\end{array}\right.$,
∴△ADM≌△ADC,
∴AM=AC=AB,
∵∠ABD=60°,
∴△AMB是等边三角形,
∴∠M=∠DCA=60°,
∵∠DOC=∠AOB,∠DCO=∠ABO=60°,
∴∠BAO=∠ODC=24°,
∴∠CAB+∠ABC+∠ACB=180°,
∴24°+2(60°+∠CBD)=180°,
∴∠CBD=18°,
故选A.
点评 本题考查等边三角形的判定和性质、全等三角形的判定和性质等知识,解决问题的关键是添加辅助线构造全等三角形,题目有点难度.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
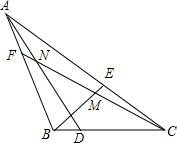 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.
如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′•OP=r2,则称点P′是点P关于⊙O的“美好点”.如图2,⊙O的半径为2,点B在⊙O上,∠BOA=60°,OA=4,若点A′、B′分别是点A,B关于⊙O的美好点,求A′B′的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
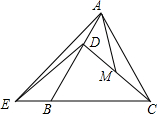 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com