

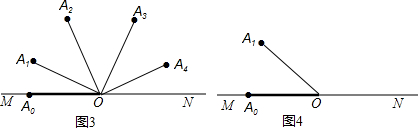

分析 (1)根据题意,明确每次旋转的角度,计算即可;
(2)根据各角的度数,找出等量关系式,列出方程,求出α的度数即可;
(3)类比第(2)小题的算法,分三种情况讨论,求出α的度数即可;
(4)无论a为多少度,旋转很多次,总会出一次OAi是∠AiOAK是的角平分线,但当a=120度时,只有两条射线,不会出现OAi是∠AiOAK是的角平分线,所以旋转会中止.
解答 解:(1)解:如图所示.aφ=45°,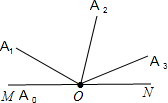
(2)解:如图所示.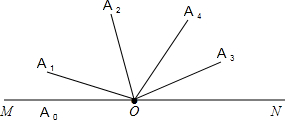
∵α<30°,
∴∠A0OA3<180°,4α<180°.
∵OA4平分∠A2OA3,
∴2(180°-6α)+$\frac{3}{2}α$=4α,解得:$α=(\frac{720}{29})^{°}$.
(3)$(\frac{20}{7})^{°}$,$(\frac{340}{13})^{°}$,($\frac{380}{13}$)°
(4)对于角α=120°不能停止.理由如下:
无论a为多少度,旋转过若干次后,一定会出现OAi是∠AiOAK是的角平分线,所以旋转会停止.
但特殊的,当a为120°时,第一次旋转120°,∠MOA1=120°,第二次旋转240°时,与OM重合,第三次旋转360°,又与OM重合,第四次旋转480°时,又与OA1重合,…依此类推,旋转的终边只会出现“与OM重合”或“与OA1重合”两种情况,不会出第三条射线,所以不会出现OAi是∠AiOAK是的角平分线这种情况,旋转不会停止.
点评 本题主要考察角度的计算的相关知识,可结合平角的性质及角度的加减进行计算分析.


科目:初中数学 来源: 题型:选择题
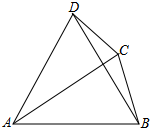 如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )
如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=78°,∠BDC=24°,则∠DBC=( )| A. | 18° | B. | 20° | C. | 25° | D. | 15° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 12或15 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com