
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

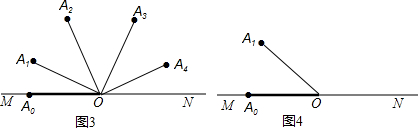

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
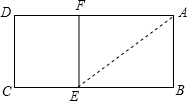 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | 4 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有两个不同型号的手机(分别记为A、B)和与之匹配的保护盖(分别记为a、b)(如图所示),散乱地放在桌子上,若从这四个物件中随机取两个,求恰好匹配的概率.
有两个不同型号的手机(分别记为A、B)和与之匹配的保护盖(分别记为a、b)(如图所示),散乱地放在桌子上,若从这四个物件中随机取两个,求恰好匹配的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com