练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．一个口袋中有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计口袋中的黄球约有多少个？

    分析 先求出试验200次摸到黄球的频率，再乘以总球的个数即可．

    解答 解：∵口袋里有25个球，试验200次，其中有120次摸到黄球，
    ∴摸到黄球的频率为：$\frac{120}{200}$=$\frac{3}{5}$，∴袋中的黄球有25×$\frac{3}{5}$=15个．
    故估计袋中的黄球有15个．

    点评 此题考查利用频率估计概率问题，关键是根据部分的具体数目=总体数目×相应频率解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．若直线y=x+b与y=2x-a的交点为（k，3），则2b+a的值为（　　）
    A．1B．2C．3D．无法计算

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．设三个互不相等的有理数，既可分别表示为1，a+b，a的形式，又可分别表示为0，$\frac{a}{b}$，b的形式，则a2008+b2009的值为2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r2，则称点P′是点P关于⊙O的“美好点”．如图2，⊙O的半径为2，点B在⊙O上，∠BOA=60°，OA=4，若点A′、B′分别是点A，B关于⊙O的美好点，求A′B′的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

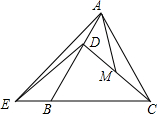    20．如图，等边△ABC中，点D在边AB上，E在CB的延长线上，已知CD=ED，M是CD中点，AM=2$\sqrt{2}$，则AE=4$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．一轮船从A地到B地需7天，而从B地到A地只需5天，则一竹排从B地漂到A地需要的天数是（　　）
    A．12B．35C．24D．47

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图1，点O是弹力墙MN上一点，魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转，当转到ON位置时，则从ON位置弹回，继续向OM位置旋转；当转到OM位置时，再从OM的位置弹回，继续转向ON位置，…，如此反复．按照这种方式将魔法棒进行如下步骤的旋转：第1步，从OA0（OA0在OM上）开始旋转α至OA1；第2步，从OA1开始继续旋转2α至OA2；第3步，从OA2开始继续旋转3α至OA3，…．

    例如：当α=30°时，OA1，OA2，OA3，OA4的位置如图2所示，其中OA3恰好落在ON上，∠A3OA4=120°； 
    当α=20°时，OA1，OA2，OA3，OA4，OA3的位置如图3所示，
    其中第4步旋转到ON后弹回，即∠A3ON+∠NOA4=80°，而OA3恰好与OA2重合．

    解决如下问题：
    （1）若α=35°，在图4中借助量角器画出OA2，OA3，其中∠A3OA2的度数是45°；
    （2）若α＜30°，且OA4所在的射线平分∠A2OA3，在如图5中画出OA1，OA2，OA3，OA4并求出α的值；

    （3）若α＜36°，且∠A2OA4=20°，则对应的α值是$（\frac{20}{7}）^{°}$，$（\frac{340}{13}）^{°}$，（$\frac{380}{13}$）°．
    （4）（选做题）当OAi所在的射线是∠AiOAk（i，j，k是正整数，且OAj与OAk不重合）的平分线时，旋转停止，请探究：试问对于任意角α（α的度数为正整数，且α=180°），旋转是否可以停止？写出你的探究思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．一元二次方程x2-x+4=0的根的情况为（　　）
    A．有两个不相等的实数根B．有两个相等的实数根
    C．只有一个实数根D．没有实数根

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．有两个不同型号的手机（分别记为A、B）和与之匹配的保护盖（分别记为a、b）（如图所示），散乱地放在桌子上，若从这四个物件中随机取两个，求恰好匹配的概率．

    查看答案和解析>>

    同步练习册答案