
【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.
(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;
(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.

【答案】(1)证明见解析;(2)PA=PB+PC.理由见解析;(3)若∠BAC=120°时,(2)中的结论不成立, ![]() PA=PB+PC.
PA=PB+PC.
【解析】试题分析:(1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;
(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;
(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.
试题解析:(1)如图①,连接PC.
∵△ACQ是由△ABP绕点A逆时针旋转得到的,
∴∠ABP=∠ACQ.
由图①知,点A、B、P、C四点共圆,
∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),
∴∠ACP+∠ACQ=180°(等量代换);
(2)PA=PB+PC.理由如下:
如图②,连接BC,延长BP至E,使PE=PC,连接CE.
∵弦AB=弦AC,∠BAC=60°,
∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).
∵A、B、P、C四点共圆,∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),
∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE=60°,
∵PE=PC,∴△PCE是等边三角形,∴CE=PC,∠E=∠ECP=∠EPC=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP(等量代换),
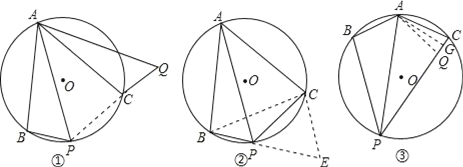
在△BEC和△APC中, 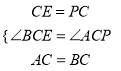 ,∴△BEC≌△APC(SAS),∴BE=PA,
,∴△BEC≌△APC(SAS),∴BE=PA,
∴PA=BE=PB+PC;
(3)若∠BAC=120°时,(2)中的结论不成立, ![]() PA=PB+PC.理由如下:
PA=PB+PC.理由如下:
如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.
∵∠BAC=120°,∠BAC+∠BPC=180°,∴∠BPC=60°.
∵弦AB=弦AC,∴∠APB=∠APQ=30°.
在△ABP和△AQP中,  ,∴△ABP≌△AQP(SAS),
,∴△ABP≌△AQP(SAS),
∴AB=AQ,PB=PQ(全等三角形的对应边相等),∴AQ=AC(等量代换).
在等腰△AQC中,QG=CG.
在Rt△APG中,∠APG=30°,则AP=2AG,PG=![]() AG,
AG,
∴PB+PC=PG﹣QG+PG+CG=PG﹣QG+PG+QG=2PG=2![]() AG,
AG,
∴![]() PA=2
PA=2![]() AG,即
AG,即![]() PA=PB+PC.
PA=PB+PC.


科目:初中数学 来源: 题型:
【题目】某城市按以下规定收取每月的煤气费:用气不超过60立方米,按每立方米0.8元收费;如果超过60立方米,超过部分按每立方米1.2元收费,已知某用户6月份煤气费平均每立方米0.88元,那么,6月份这位用户应交煤气费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一块长为30m,宽为24m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为多少米.

查看答案和解析>>
科目:初中数学 来源: 题型:
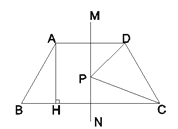
【题目】如图,题型ABCD中,AD∥BC,AD=CD=AD=2,∠B=60°,AH⊥BC于点H,且AH=![]() ,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
,直线MN是梯形的对称轴,P为直线MN上的一动点,则PC+PD的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
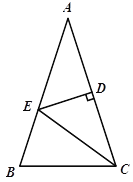
【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块长18米,宽15米的矩形荒地修建成一个花园(阴影部分)所占的面积为原来荒地面积的三分之二.(精确到0.1m)
(1)设计方案1(如图1)花园中修两条互相垂直且宽度相等的小路.
(2)设计方案2(如图2)花园中每个角的扇形都相同.
以上两种方案是否都能符合条件?若能,请计算出图1中的小路的宽和图2中扇形的半径;若不能符合条件,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有一个内角是锐角的三角形是锐角三角形B.钝角三角形的三个内角都是钝角
C.有一个内角是直角的三角形是直角三角形D.三条边都相等的三角形称为等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com