
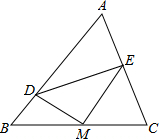
 如图,在△ABC中,经过BC的中点M,有垂直相交于M的两条直线,它们与AB、AC分别交于D、E,求证:BD+CE>DE.
如图,在△ABC中,经过BC的中点M,有垂直相交于M的两条直线,它们与AB、AC分别交于D、E,求证:BD+CE>DE. 分析 延长DM到F,使MF=DM,连接EF、CF,易证△BDM≌△CFM(SAS),所以BD=CF,易证△DEM≌△FEM(SAS),所以DE=FE,在△ECF中,EC+FC>EF,即可得解.
解答 证明:如图,延长DM到F,使MF=DM,连接EF、CF,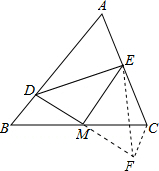
在△BDM和△CFM中
$\left\{\begin{array}{l}{BM=CM}\\{∠BMD=∠CMF}\\{DM=FM}\end{array}\right.$
∴△BDM≌△CFM(SAS),
∴BD=CF,
在△DEM和△FEM中
$\left\{\begin{array}{l}{DM=FM}\\{∠EMD=∠EMF=90°}\\{EM=EM}\end{array}\right.$,
∴△DEM≌△FEM(SAS),
∴DE=FE,
在△ECF中,EC+FC>EF,
∴BD+EC>DE.
点评 此题主要考查全等三角形的判定和性质以及三角形三边之间的关系,作辅助线构成全等三角形是关键.


科目:初中数学 来源: 题型:选择题
| A. | 2:3 | B. | 1:2 | C. | 1:3 | D. | 3:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班,王叔叔某天骑自行车上班,从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).
“低碳生活,绿色出行”的理念正逐渐被人们所接受,越来越多的人选择骑自行车上下班,王叔叔某天骑自行车上班,从家出发到单位过程中行进速度v(米/分钟)随时间t(分钟)变化的函数图象大致如图所示,图象由三条线段OA、AB和BC组成.设线段OC上有一动点T(t,0),直线l过点T且与横轴垂直,梯形OABC在直线l左侧部分的面积即为t分钟内王叔叔行进的路程s(米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
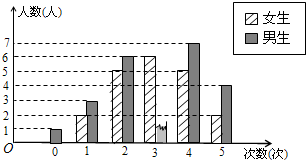 为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).| 统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
| 该班级男生 | 3 | 3 | 4 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com