
【题目】如图,在![]() ABCD中,E为对角线AC延长线上的一点.
ABCD中,E为对角线AC延长线上的一点.
(1)若四边形ABCD是菱形,求证:BE=DE.
(2)写出(1)的逆命题,并判断其是真命题还是假命题,若是真命题,给出证明;若是假命题,举出反例.

【答案】见解析
【解析】试题分析:(1)根据“菱形ABCD的对角线互相垂直平分”的性质推知OE是△BDE的边BD上的中垂线,结合角平分线的性质可知△DEB为等腰三角形;
(2)(1)的逆命题是“若BE=DE,则四边形ABCD是菱形”.根据平行四边形ABCD的对角线相互平分知OD=OB,结合角平分线的性质推知OE是BD的中垂线,即平行四边形ABCD的对角线互相垂直.
试题解析:(1)连接BD,交AC于点O,

∵四边形ABCD是菱形,
∴AC⊥BD,且BO=OD.
又∵E是AC延长线上的一点,
∴EO是△BDE的边BD的中垂线,∠DEB的角平分线,
∴△DEB是等腰三角形,
∴BE=DE;
(2)(1)的逆命题是“若BE=DE,则四边形ABCD是菱形”,
它是真命题,理由如下:
∵平行四边形ABCD,对角线AC、BD交于点O,
∴BO=OD.
又∵BE=DE
∴EO⊥BD,即AC⊥BD,
∴四边形ABCD是菱形。


科目:初中数学 来源: 题型:
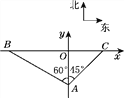
【题目】在某段限速公路BC上(公路视为直线),交通管理部门规定汽车的最高行驶速度不能超过60 km/h(即![]() ),并在离该公路100 m处设置了一个监测点A.在如图的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.另外一条公路在y轴上,AO为其中的一段.
),并在离该公路100 m处设置了一个监测点A.在如图的平面直角坐标系中,点A位于y轴上,测速路段BC在x轴上,点B在点A的北偏西60°方向上,点C在点A的北偏东45°方向上.另外一条公路在y轴上,AO为其中的一段.
(1)求点B和点C的坐标;
(2)一辆汽车从点B匀速行驶到点C所用的时间是15 s,通过计算,判断该汽车在这段限速路上是否超速.(参考数据: ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次美化校园活动中,先安排32人去拔草,18人去植树,后又增派20人去支援他们,结果拔草的人数是植树人数的2倍、问支援拔草和支援植树的分别有多少人?若设支援拔草的有x人,则下列方程中正确的是( )
A.32+x=2×18
B.32+x=2(38﹣x)
C.52﹣x=2(18+x)
D.52﹣x=2×18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,王华同学按下列步骤作图:(1)以点O为圆心,任意长为半径作弧,交OA于点C,交OB于点D,分别以点C、点D为圆心,大于![]() CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于
CD的长为半径作弧,两弧交于点E,作射线OE;(2)在射线OE上取一点F,分别以点O、点F为圆心,大于![]() OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )
OF的长为半径作弧,两弧交于两点G、H,作直线GH,交OA于点M,交OB于点N;(3)连接FM、FN.那么四边形OMFN一定是( )
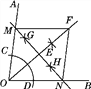
A. 梯形 B. 矩形 C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,ABCD中,点E,F在直线AC上(点E在F左侧),BE∥DF.

(1)求证:四边形BEDF是平行四边形;
(2)若AB⊥AC,AB=4,BC=![]() ,当四边形BEDF为矩形时,求线段AE的长.
,当四边形BEDF为矩形时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小明站在路灯P的底下观察自己的影子时发现,当他站在F点的位置时,在地面上的影子为BF,小明向前走2米到D点时,在地面上的影子为AD,若AB=4米,∠PBF=60°,∠PAB=30°,通过计算,求出小明的身高.(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com