

分析 (1)根据SAS证明△EAC与△DAB全等,再利用全等三角形的性质解答即可;
(2)利用全等三角形的性质得出∠ECA=∠DBA,进而解答即可;
(3)根据(1)(2)中的证明步骤解答即可.
解答 解:(1)CE=BD,理由如下:
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB=90°}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°-90°=90°;
(3)成立,
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAC=∠DAB=90°}\\{AC=AB}\end{array}\right.$,
∴△EAC≌△DAB(SAS),
∴CE=BD;
∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°-90°=90°.
点评 本题主要考查了全等三角形的判定及其性质、等腰直角三角形的性质,解题的关键是牢固掌握全等三角形的判定及其性质知识点.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
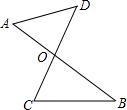 如图,线段AB、CD相交于点O,连接AD、CB.
如图,线段AB、CD相交于点O,连接AD、CB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应聘者 | 笔试 | 口试 | 得票 |
| 甲 | 85 | 83 | 90 |
| 乙 | 80 | 85 | 92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
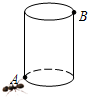 如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).
如图所示.有一个圆柱.它的高等于12厘米.底面半径等于$\frac{5}{6}$厘米.在圆柱下底面的A点有一只蚂蚁.它想吃到上底面B点处的食物.沿圆柱侧面爬行的最短路程是多少?(π的值取3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com