
分析 (1)①已知两对值代入T中计算求出a与b的值;
②利用已知得出关于m的等式求出答案;
③根据题中新定义化简已知不等式,根据不等式组恰好有2个整数解,求出p的范围即可;
(2)由T(x,y)=T(y,x)列出关系式,整理后即可确定出a与b的关系式.
解答 解:(1)①∵T(1,-1)=1,T(3,1)=-1,
∴$\left\{\begin{array}{l}{a-b=2}\\{3a+b=-10}\end{array}\right.$,
∴a=-2,b=-4.
②∵T(x,y)=$\frac{ax+by}{3x+y}$,T(x,x2)=T(x2,x),
∴$\frac{-2x-4{x}^{2}}{3x+{x}^{2}}$=$\frac{-2{x}^{2}-4x}{3{x}^{2}+x}$,
∵x≠0,
∴$\frac{1+2x}{3+x}$=$\frac{x+2}{3x+1}$,
∴x2=1,x=±1,
经检验x=±1是原方程的解.
③∵$\left\{\begin{array}{l}{T(2m,5-6m)<4}\\{T(m,3-3m)≥p}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\frac{20m-20}{5}<4}\\{\frac{10m-12}{3}≥p}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m<2}\\{m≥\frac{12+3p}{10}}\end{array}\right.$,
∵只有两个整数解,
∴-1<$\frac{12+3p}{10}$≤0,
∴-$\frac{22}{3}$<p≤-4.
(2)∵(2)由T(x,y)-T(y,x)=0,
∴$\frac{ax+by}{3x+y}$-$\frac{ay+bx}{3y+x}$=0,
整理得:(x2-y2)(a-3b)=0,
∵T(x,y)=T(y,x)对任意实数x,y都成立,
∴a-3b,即a=3b.
点评 此题考查了不等式组的实际运用,分式的混合运算,解二元一次方程组,以及一元一次不等式组的整数解,弄清题中的新定义是解本题的关键.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
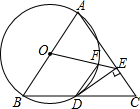 如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.
如图.△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
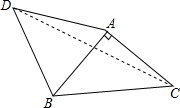 已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.
已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则AC=2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com