Question

17．如图：已知等边△ABC的边长为2，P是BC边上的任一点（与B、C不重合），连接AP，以AP为边向两侧作等边△APD和等边△APE，分别与边AB、AC交于点M、N（如图1）．
（1）求证：AM=AN；
（2）连接DE分别与边AB、AC交于点G、H，如图2，当∠BAD是多少度时，AD=DH？
（3）在（2）的条件下，以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形，并说明理由．

Answer 1

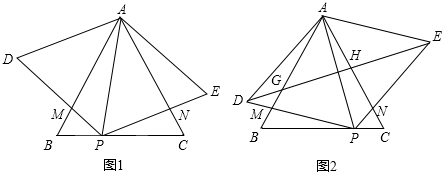
分析 （1）由已知条件可以得出AD=AP，∠DAP=∠BAC=60°，∠ADM=∠APN=60°，从而得出∠DAM=∠PAN，可以得出△ADM≌△APN，就可以得出结论．
（2）根据等边三角形的性质和三角形内角和定理求出∠DAH=∠AHD，根据等腰三角形的性质求出即可；
（3）以DG、GH、HE这三条线段为边构成的三角形为直角三角形，由已知条件可知四边形ADPE为菱形，可以得到∠ADO=∠AEH=30°，根据∠DAB的度数可以求出∠AGO、∠HAO、，∠EAH的度数．设AO=a，得出DG=（$\sqrt{3}$-1）a，求出∠DHA=∠DAH=75°，求得GH=（3-$\sqrt{3}$）a，HE=2（$\sqrt{3}$-1）a，最后由勾股定理的逆定理就可以得出结论．

解答 解：（1）证明：∵△ABC、△APD和△APE是等边三角形，
∴AD=AP，∠DAP=∠BAC=60°，∠ADM=∠APN=60°，
∴∠DAM=∠PAN．
在△ADM和△APN中，
∵$\left\{\begin{array}{l}{∠DAM=∠PAN}\\{AD=AP}\\{∠ADM=∠APN}\end{array}\right.$，
∴△ADM≌△APN，
∴AM=AN；

（2）当∠BAD=15°时，AD=DH，
理由是：∵△ADP和△APE是等边三角形，
∴AD=AP=AE，∠DAP=∠EAP=60°，
∴∠ADE=∠AED=$\frac{1}{2}$×（180°-60°-60°）=30°，
∵由（1）知：△ADM≌△APN，
∴∠BAD=∠CAP=15°，
∴∠BAP=∠EAC=60°-15°=45°，
∴∠DAH=∠BAD+∠CAB=15°+60°=75°，
∴∠AHD=180°-∠ADH-∠DAH=180°-30°-75°=75°，
∴∠DAH=∠AHD，
∴AD=DH，
即当∠BAD=15°时，AD=DH；

（3）以DG、GH、HE这三条线段为边构成的三角形为直角三角形．
解：设DE交AP于点O，
∵△APD和△APE是等边三角形，
∴AD=DP=AP=PE=EA，
∴四边形ADPE为菱形，
∴AO⊥DE，∠ADO=∠AEH=30°．
∵∠DAB=15°，
∴∠GAO=45°，
∴∠AGO=45°，∠HAO=15°，
∴∠EAH=45°，
设AO=a，则AD=AE=2a，GO=AO=a，OD=$\sqrt{3}$a．
∴DG=DO-GO=（$\sqrt{3}$-1）a．
∵∠DAB=15°，∠BAC=60°，∠ADO=30°，
∴∠DHA=∠DAH=75°．
∴DH=AD=2a，
∴GH=DH-DG=2a（$\sqrt{3}$-1）a=（3-$\sqrt{3}$）a．
HE=DE-DH=2DO-DH=2 $\sqrt{3}$a-2a．
∵DG²+GH²=[（$\sqrt{3}$-1）a]²+[（3-$\sqrt{3}$）a]²=（16-8$\sqrt{3}$）a²，
HE²=（2$\sqrt{3}$-2a）²=（16-8$\sqrt{3}$）a²，
∴DG²+GH²=HE²，
∴以DG、GH、HE这三条线段为边构成的三角形为直角三角形．

点评 本题考查了等边三角形的性质，菱形的性质和判定，线段垂直平分线的判定，勾股定理的运用．本题的综合性较强，在解答时要注意解答问题的突破口，这也是解答问题的关键．