
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.
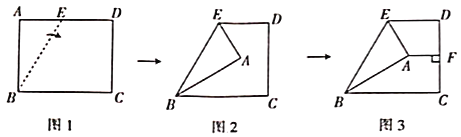
(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD的四个顶点都在⊙O上,对角线AC和BD交于点E.
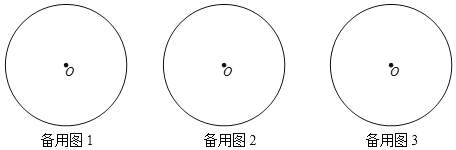
(1)若∠BAD和∠BCD的度数之比为1:2,求∠BCD的度数;
(2)若AB=3,AD=5,∠BAD=60°,点C为劣弧BD的中点,求弦AC的长;
(3)若⊙O的半径为1,AC+BD=3,且AC⊥BD.求线段OE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
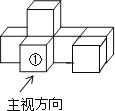
A. 主视图不变,左视图不变
B. 左视图改变,俯视图改变
C. 主视图改变,俯视图改变
D. 俯视图不变,左视图改变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求这个二次函数的表达式;
(2)若![]() 是直线
是直线![]() 上方抛物线上一点;
上方抛物线上一点;
①当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 的夹角是
的夹角是![]() 的两倍,若存在,直接写出点
的两倍,若存在,直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 内接三角形,点D是BC的中点,请仅用无刻度的直尺,分别按下列要求画图.
内接三角形,点D是BC的中点,请仅用无刻度的直尺,分别按下列要求画图.
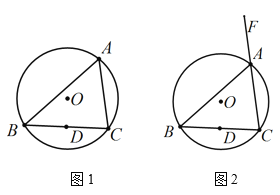
(1)如图1,画出弦AE,使AE平分∠BAC;
(2)如图2,∠BAF是![]() 的一个外角,画出∠BAF的平分线.
的一个外角,画出∠BAF的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(1﹣m)x2﹣mx﹣1与x轴交于A、B两点,顶点为P.
(1)求m的取值范围;
(2)若A、B位于原点两侧,求m的取值范围;
(3)若顶点P在第四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com