
分析 ①根据有理数的乘法、除法、减法进行计算即可;
②根据有理数的乘除和加减进行计算即可.
解答 解:①(-$\frac{2}{3}$)×$\frac{1}{4}$-|-4|3÷(-2)4
=$-\frac{1}{6}-64×\frac{1}{16}$
=-$\frac{1}{6}-4$
=$-4\frac{1}{6}$;
②25×$\frac{3}{4}$-(-25)×$\frac{1}{2}$+(-$\frac{1}{4}$)×25.
=$\frac{75}{4}+\frac{25}{2}-\frac{25}{4}$
=25.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的法则.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
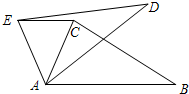 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
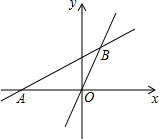 如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.
如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲 | 8 | 6 | 7 | 8 | 9 | 10 | 6 | 5 | 4 | 7 |
| 乙 | 7 | 9 | 8 | 5 | 6 | 7 | 7 | 6 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com