平面直角坐标系中.有A.B.C三点.其中A为原点.点B和点C的坐标分别为．(1)证明:△ABC为Rt△．(2)请你在直角坐标系中找一点D.使得△ABC与△ABD相似.写出所有满足条件的点D的坐标.并在同一坐标系中画出所有符合要求的三角形．题所作的图中.连接任意两个直角三角形的直角顶点均可得到一条线段.在连接两点所得的所有线段中任取一条线段.求取到长� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

4．平面直角坐标系中，有A、B、C三点，其中A为原点，点B和点C的坐标分别为（5，0）和（1，2）．
（1）证明：△ABC为Rt△．
（2）请你在直角坐标系中找一点D，使得△ABC与△ABD相似，写出所有满足条件的点D的坐标，并在同一坐标系中画出所有符合要求的三角形．
（3）在第（2）题所作的图中，连接任意两个直角三角形（包括△ABC）的直角顶点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，求取到长度为无理数的线段的概率．

分析（1）过点C作CH⊥x轴于H，如图1，只需运用勾股定理求出AB²、AC²、BC²，然后运用勾股定理的逆定理就可解决问题；
（2）△ABC与△ABD相似，对应关系不确定，故需分六种情况（①若△ABC∽△ABD，②若△ABC∽△BAD，③若△ABC∽△ADB，④若△ABC∽△DAB，⑤若△ABC∽△BDA，⑥若△ABC∽△DBA）讨论，然后运用相似三角形的性质就可解决问题；
（3）图中的直角三角形的直角顶点有A、B、C、D₁、D₂、D₃，只需求出任意两直角顶点的连线段的条数和长度为无理数的线段的条数，就可解决问题．

解答解：（1）过点C作CH⊥x轴于H，如图1，

∵A（0，0），B（5，0），C（1，2），
∴AC²=1²+2²=5，BC²=（5-1）²+2²=20，AB²=5²=25，
∴AB²=AC²+BC²，
∴△ABC为Rt△；

（2）①若△ABC∽△ABD，则有D₁（1，-2）；
②若△ABC∽△BAD，则有D₂（4，-2），D₃（4，2）；
③若△ABC∽△ADB，则有D₄（5，-10），D₅（5，10）；
④若△ABC∽△DAB，则有D₆（5，-2.5），D₇（5，2.5）；
⑤若△ABC∽△BDA，则有D₈（0，-10），D₉（0，10）；
⑥若△ABC∽△DBA，则有D₁₀（0，-2.5），D₁₁（0，2.5）；
所有符合要求的三角形如图所示．

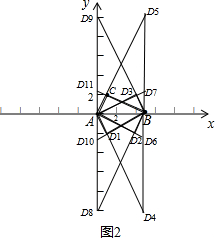
（3）图中的直角三角形的直角顶点有A、B、C、D₁、D₂、D₃．
任意两直角顶点的连线段共有$\frac{6×5}{2}$=15条，
其中AB=5，CD₁=D₂D₃=4，CD₂=D₁D₃=5，CD₃=D₁D₂=3，
故长度为有理数的线段共7条，长度为无理数的线段共8条，
则取到长度为无理数的线段的概率为p=$\frac{8}{15}$．

点评本题主要考查了勾股定理及其逆定理、相似三角形的性质、概率公式等知识，运用分类讨论的思想是解决第（2）小题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>