
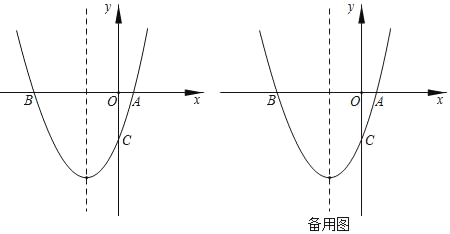
【题目】如图,抛物线y=ax2+2x﹣3a经过A(1,0)、B(b,0)、C(0,c)三点.
(1)求b,c的值;
(2)在抛物对称轴上找一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)b=﹣3;(2)P(﹣1,﹣2);(3)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.符合条件的点N的坐标为(﹣2,﹣3),(﹣1+![]() ,3)或(﹣1﹣
,3)或(﹣1﹣![]() ,3).
,3).
【解析】
(1)先把A(1,0)代入抛物线y=ax2+2x﹣3a,求出a的值,然后再分别把B(b,0)、C(0,c)的值代入即可求出b,c的值;
(2)根据轴对称的性质找出点P的位置,然后求出直线BC的解析式和对称轴方程,二者联立可求出点P的坐标;
(3)分当点N在x轴下方时和当点N在x轴上方时两种情况求解即可.
解:(1)把A(1,0)代入抛物线y=ax2+2x﹣3a,
可得:a+2﹣3a=0
解得a=1.
∴抛物线的解析式为:y=x2+2x﹣3;
把B(b,0),C(0,c)代入y=x2+2x﹣3,
可得:b=1或b=﹣3,c=﹣3,
∵A(1,0),
∴b=﹣3;
(2)∵抛物线的解析式为:y=x2+2x﹣3,
∴其对称轴为直线x=﹣![]() =﹣1,
=﹣1,
连接BC,如图1所示,
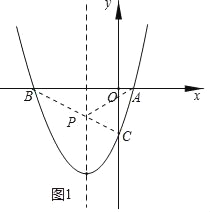
∵B(﹣3,0),C(0,﹣3),
∴设直线BC的解析式为y=kx+b(k≠0),
∴![]() ,
,
解得![]() ,
,
∴直线BC的解析式为y=﹣x﹣3,
当x=﹣1时,y=1﹣3=﹣2,
∴P(﹣1,﹣2);
(3)存在点N,使以A,C,M,N四点构成的四边形为平行四边形.
如图2所示,
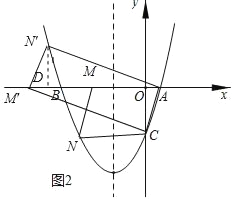
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=﹣1,C(0,﹣3),
∴N1(﹣2,﹣3);
②当点N在x轴上方时,
如图2,过点N'作N'D⊥x轴于点D,
在△AN'D与△M'CO中,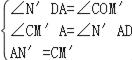
∴△AN'D≌△M'CO(AAS),
∴N'D=OC=3,即N'点的纵坐标为 3.
∴3=x2+2x﹣3,
解得x=﹣1+![]() 或x=﹣1﹣
或x=﹣1﹣![]() ,
,
∴N'(﹣1+![]() ,3),N“(﹣1﹣
,3),N“(﹣1﹣![]() ,3).
,3).
综上所述,符合条件的点N的坐标为(﹣2,﹣3),(﹣1+![]() ,3)或(﹣1﹣
,3)或(﹣1﹣![]() ,3).
,3).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
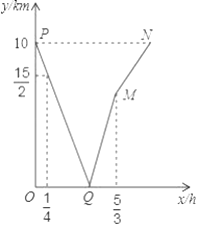
【题目】甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发x h后,两人相距y km,图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该品种苹果,但这次的进货价比试销时每千克多了0.2元,购进苹果数量是试销的2倍.
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种苹果按每千克5元的定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段![]() 、
、![]() 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程![]() (米)与所用时间
(米)与所用时间![]() (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
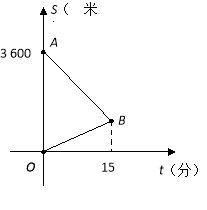
【1】求点![]() 的坐标和
的坐标和![]() 所在直线的函数关系式
所在直线的函数关系式
【2】小明能否在比赛开始前到达体育馆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究与证明)
在正方形ABCD中,G是射线AC上一动点(不与点A、C重合),连BG,作BH⊥BG,且使BH=BG,连GH、CH.
(1)若G在AC上(如图1),则:①图中与△ABG全等的三角形是 .
②线段AG、CG、GH之间的数量关系是 .
(2)若G在AC的延长线上(如图2),那么线段AG、CG、BG之间有怎样的数量关系?写出结论并给出证明;
(应用)(3)如图3,G在正方形ABCD的对角线CA的延长线上,以BG为边作正方形BGMN,若AG=2,AD=4,请直接写出正方形BGMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】题目:如图①,在四边形ABCD中,AB=AD,∠ABC=∠ADC,那么BC=CD吗?请说明理由.

小明的作法如下:
如图②,连结AC.
∵AB=AD,∠ABC=∠ADC,AC=AC.
∴△ABC≌△ADC.
∴BC=CD.
(1)小明的作法错误的原因是 .
(2)请正确解答这道题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+b的图象与x轴交于点A(2,0),与反比例函数y=![]() 的图象交于点B(3,n).
的图象交于点B(3,n).
(1)求一次函数与反比例函数的表达式;
(2)若点P为x轴上的点,且△PAB的面积是2,则点P的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
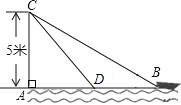
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com