
【题目】如图,抛物线与x轴相交于A、B两点,与y轴的交于点C,其中A点的坐标为(﹣3,0),点C的坐标为(0,﹣3),对称轴为直线x=﹣1.
(1)求抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

【答案】(1)y=x2+2x﹣3;(2)点P的坐标为(4,21)或(﹣4,5);(3)![]() .
.
【解析】
(1)先根据点A坐标及对称轴得出点B坐标,再利用待定系数法求解可得;
(2)利用(1)得到的解析式,可设点P的坐标为(a,a2+2a﹣3),则点P到OC的距离为|a|.然后依据S△POC=4S△BOC列出关于a的方程,从而可求得a的值,于是可求得点P的坐标;
(3)先求得直线AC的解析式,设点D的坐标为(x,x2+2x﹣3),则点Q的坐标为(x,﹣x﹣3),然后可得到QD与x的函数的关系,最后利用配方法求得QD的最大值即可.
解:(1)∵抛物线与x轴的交点A(﹣3,0),对称轴为直线x=﹣1,
∴抛物线与x轴的交点B的坐标为(1,0),
设抛物线解析式为y=a(x+3)(x﹣1),
将点C(0,﹣3)代入,得:﹣3a=﹣3,
解得a=1,
则抛物线解析式为y=(x+3)(x﹣1)=x2+2x﹣3;
(2)设点P的坐标为(a,a2+2a﹣3),则点P到OC的距离为|a|.
∵S△POC=4S△BOC,
∴![]() OC|a|=4×
OC|a|=4×![]() OCOB,即
OCOB,即![]() ×3×|a|=4×
×3×|a|=4×![]() ×3×1,解得a=±4.
×3×1,解得a=±4.
当a=4时,点P的坐标为(4,21);
当a=﹣4时,点P的坐标为(﹣4,5).
∴点P的坐标为(4,21)或(﹣4,5).
(3)如图所示:
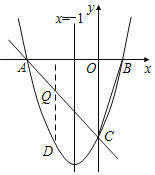
设AC的解析式为y=kx﹣3,将点A的坐标代入得:﹣3k﹣3=0,解得k=﹣1,
∴直线AC的解析式为y=﹣x﹣3.
设点D的坐标为(x,x2+2x﹣3),则点Q的坐标为(x,﹣x﹣3).
∴QD=﹣x﹣3﹣( x2+2x﹣3)=﹣x﹣3﹣x2﹣2x+3=﹣x2﹣3x=﹣(x2+3x+![]() ﹣
﹣![]() )=﹣(x+
)=﹣(x+![]() )2+
)2+![]() ,
,
∴当x=﹣![]() 时,QD有最大值,QD的最大值为
时,QD有最大值,QD的最大值为![]() .
.


科目:初中数学 来源: 题型:
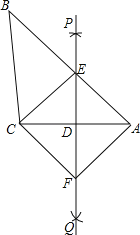
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若ED=6,AE=10,则菱形AECF的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
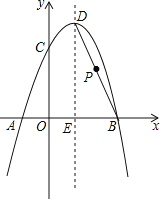
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里有1个红球和n个白球,它们除颜色外其余都相同.
(1)从这个袋子里摸出一个球,记录其颜色,然后放回,摇均匀后,重复该实验,经过大量实验后,发现摸到白球的频率稳定于![]() 左右,求n的值;
左右,求n的值;
(2)在(1)的条件下,先从这个袋中摸出一个球,记录其颜色,放回,摇均匀后,再从袋中摸出一个球,记录其颜色.请用画树状图或者列表的方法,求出先后两次摸出不同颜色的两个球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是对角线BD上一动点.
(1)如图1,当CE⊥BD时,求DE的长;
(2)如图2,作EM⊥EN分别交边BC于M,交边CD于N,连MN.
①若![]() ,求tan∠ENM;
,求tan∠ENM;
②若E运动到矩形中心O,连CO.当CO将△OMN分成两部分面积比为1:2时,直接写出CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com