
【题目】在矩形ABCD中,AB=6,AD=8,点E是对角线BD上一动点.
(1)如图1,当CE⊥BD时,求DE的长;
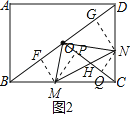
(2)如图2,作EM⊥EN分别交边BC于M,交边CD于N,连MN.
①若![]() ,求tan∠ENM;
,求tan∠ENM;
②若E运动到矩形中心O,连CO.当CO将△OMN分成两部分面积比为1:2时,直接写出CN的长.

【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]() .
.
【解析】
(1)由矩形性质可求得对角线BD=10,由CE⊥BD得∠CED=∠BCD=90°,再由公共角∠CDE=∠BDC得△CDE∽△BDC,由对应边成比例并把数值代入即求得DE的长.
(2)①由![]() 和BD=10求得DE=
和BD=10求得DE=![]() ,BE=
,BE=![]() .分别过点M、N作BD的垂线段MF、NG,设MF=a,NG=b,易证△FBM∽△CBD和△GDN∽△CDB,利用对应边成比例得到用a表示BF、用b表示DG的式子,进而得到用a表示的EF、用b表示的EG.又由EM⊥EN易证△EMF∽△NEG,得到
.分别过点M、N作BD的垂线段MF、NG,设MF=a,NG=b,易证△FBM∽△CBD和△GDN∽△CDB,利用对应边成比例得到用a表示BF、用b表示DG的式子,进而得到用a表示的EF、用b表示的EG.又由EM⊥EN易证△EMF∽△NEG,得到![]() ,利用后两个比值把含a、b的式子代入求得a与b之间的关系,再代回去即求得tan∠ENM=
,利用后两个比值把含a、b的式子代入求得a与b之间的关系,再代回去即求得tan∠ENM=![]() 的值.
的值.
②先由①的证明过程求得![]() ;过点M作MP⊥OC于点P,过点N作NQ⊥OC于点Q,构造△MOP∽△ONQ,所以有
;过点M作MP⊥OC于点P,过点N作NQ⊥OC于点Q,构造△MOP∽△ONQ,所以有![]() .易证△NCQ∽△BDC,设CN=5x,则可利用对应边成比例得到NQ=4x、CQ=3x,进而得OQ=5﹣3x.CO将△OMN分成△OMH和△ONH,两部分面积比为1:2,若以OH为底,则他们的高MP和NQ的比为1:2或2:1,进而可用x表示MP的长.把用x表示的MP、OQ代入
.易证△NCQ∽△BDC,设CN=5x,则可利用对应边成比例得到NQ=4x、CQ=3x,进而得OQ=5﹣3x.CO将△OMN分成△OMH和△ONH,两部分面积比为1:2,若以OH为底,则他们的高MP和NQ的比为1:2或2:1,进而可用x表示MP的长.把用x表示的MP、OQ代入![]() ,即求得x的值,进而得CN的长.
,即求得x的值,进而得CN的长.
解:(1)∵矩形ABCD中,AB=6,AD=8
∴∠BCD=90°,BC=AD=8,CD=AB=6
∴BD=![]() =10
=10
∵CE⊥BD
∴∠CED=∠BCD=90°
∵∠CDE=∠BDC
∴△CDE∽△BDC
∴![]()
∴DE=![]()
(2)①如图1,过点M作MF⊥BD于点F,过点N作NG⊥BD于点G
∵![]() ,BD=10
,BD=10
∴BD=BE+DE=3DE+DE=4DE=10
∴DE=![]() ,BE=
,BE=![]()
设MF=a,NG=b
∵∠BFM=∠C=90°,∠FBM=∠CBD
∴△FBM∽△CBD
∴![]()
∴BF=![]() =
=![]() a
a
∴EF=BE﹣BF=![]() a
a
同理可证:△GDN∽△CDB
∴![]()
∴DG=![]() =
=![]() b
b
∴EG=DE﹣DG=![]() b
b
∵EM⊥EN
∴∠MEN=∠MFE=∠NGE=90°
∴∠MEF+∠NEG=∠MEF+∠EMF=90°
∴∠EMF=∠NEG
∴△EMF∽△NEG
∴![]()
∴EFEG=NGMF
∴(![]() a)(
a)(![]() b)=ba
b)=ba
整理得:16a=90﹣27b
∴在Rt△MEN中,tan∠ENM=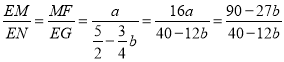 =
=![]()
②如图2,过点M作MF⊥BD于点F,MP⊥OC于点P,过点N作NG⊥BD于点G,NQ⊥OC于点Q,设OC与MN交点为H
∵点O为矩形中心,BD=10
∴OB=OD=OC=
由①可得,设MF=a,NG=b,则BF=![]() =
=![]() a,DG=
a,DG=![]() =
=![]() b,OFOG=NGMF
b,OFOG=NGMF
∴OF=OB﹣BF=5﹣![]() a,OG=OD﹣DG=5﹣
a,OG=OD﹣DG=5﹣![]() b
b
∴(5﹣![]() a)(5﹣
a)(5﹣![]() b)=ab
b)=ab
整理得:16a=60﹣9b
∴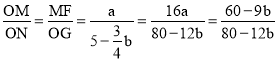 =
=![]()
设CN=5x
∵∠NCQ=∠BDC,∠NQC=∠BCD=90°
∴△NCQ∽△BDC
∴![]() =
=![]()
∴CQ=![]() CN=3x,NQ=
CN=3x,NQ=![]() CN=4x
CN=4x
∴OQ=OC﹣CQ=5﹣3x
∵∠MPO=∠MON=∠OQN=90°
∴∠MOP+∠NOQ=∠NOQ+∠ONQ=90°
∴∠MOP=∠ONQ
∴△MOP∽△ONQ
∴![]()
(i)若S△OMH=2S△ONH,且两三角形都以OH为底
∴MP=2NQ=8x
∴![]()
解得:x=![]()
∴CN=![]()
(ii)若2S△OMH=S△ONH,则MP=![]() NQ=2x
NQ=2x
∴![]()
解得:x=![]()
∴CN=![]()
综上所述,CN的长为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴相交于A、B两点,与y轴的交于点C,其中A点的坐标为(﹣3,0),点C的坐标为(0,﹣3),对称轴为直线x=﹣1.
(1)求抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,-2,-3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再随机取出一个小球,记下数字为y.
(1)小明抽到的数字是负数的概率是 .
(2)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(3)求小明两次取出小球的数字都为正数的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于点A,B两点,点A在点B的左侧,点M为AB的中点,PQ![]() x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.
x轴交抛物线于点P,Q,点P在点Q的左侧,点Q在第一象限,以PQ,PM为邻边作PMNQ.设点P的横坐标为m.

(1)当m=0时,求PMNO的周长;
(2)连结MQ,若MQ⊥QN时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题:
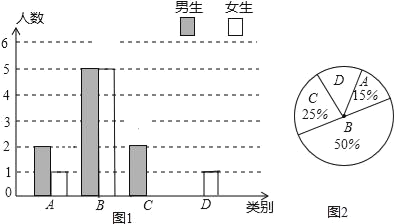
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“a2≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,∴(x+2)2+1≥1,∴x2+4x+5≥1.试利用“配方法”解决下列问题:
(1)填空:因为x2-4x+7=(x-_____)2+______,所以当x=_____时,代数式x2-4x+7有最_____(填“大”或“小”)值,这个最值为_______;
(2)比较代数式x2-2与6x-13的大小.
(3)试求2x2-3x+2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com