
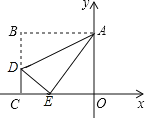
【题目】如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上,点D在边BC上,将该矩形沿AD折叠,点B恰好落在边OC上的E处,且△CDE为等腰直角三角形,若OA=4,则点D的坐标是_____.
科目:初中数学 来源: 题型:
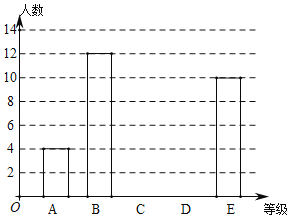
【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了本校九年级300名学生到校的方式,根据调査结果绘制出统计图的一部分如图:
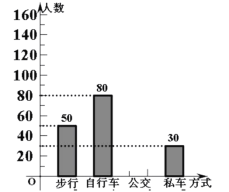
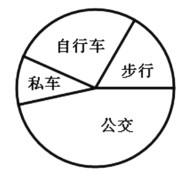
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)请估计在全校1200名学生中乘公交的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象在第一象限交于点
的图象在第一象限交于点![]() ,连接
,连接![]() ,且
,且![]() .则不等式
.则不等式![]() 的解集为( )
的解集为( )
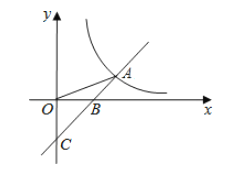
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.-3<x<0或x>3
D.-3<x<0或x>3
查看答案和解析>>
科目:初中数学 来源: 题型:
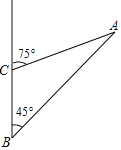
【题目】青白江凤凰湖湿地公园是一处具有国际水准的旅游度假区,以生态、休闲、水景环境及具有多国风情的建筑为特色.如图为凤凰湖湿地公园三个景点A,B,C的平面示意图,景点C在B的正北方向4千米处,景点A在B的东北方向,在C的北偏东75°方向上,求景点A、B之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解本校学生的预防新型冠状病毒知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查,调查结果按了解程度分为“非常了解”、“了解”、“了解较少”、“不了解”四类,并将调査结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:

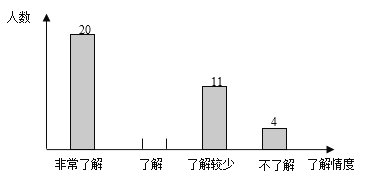
(1)本次调查的学生共有多少人?
(2)估计该校2000名学生中“了解”的人数约有多少人?
(3)若“不了解”的4人中有甲、乙两名男生,丙、丁两名女生,从这4人中随机抽取两人去重新参加预防新冠病毒如识培训,请用画树状图或列表的方法,求恰好抽到2名男生的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P为∠MON的平分线上一点,以P点为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA·OB=OP2,我们就把∠APB叫作∠MON的智慧角.
(1)如图②,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°,求证:∠APB是∠MON的智慧角;
(2)如图①,已知∠MON=α(0°<α<90°),OP=2,若∠APB是∠MON的智慧角,连接AB,用含α的式子分别表示∠APB的度数和△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
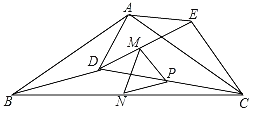
【题目】已知,△ABC和△ADE均为等腰三角形,AB=AC=5,AD=AE=2,且∠BAC=∠DAE=120°,把△ADE绕点A在平面内自由旋转.如图,连接BD,CD,CE,点M,P,N分别为DE,DC,BC的中点,连接MP,PN,MN,则△PMN的面积最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com