练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知2x2+3y2-8x+6y+11=0，x+y=1．

    分析 将等式的左边通过配方重新组合，配成两个非负数的和，借助非负数的性质求出x、y的值即可解决问题．

    解答 解：2x2+3y2-8x+6y+11=0
    2x2-8x+8+3y2+6y+3=0
    2（x-2）2+3（y+1）2=0
    ∴x=2，y=-1，
    ∴x+y=2-1=1；
    故答案为：1．

    点评 本题考查了配方法、非负数的性质及其应用问题；将所给等式的左边配成两个非负数和的形式是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

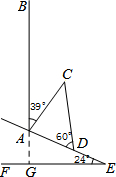    17．如图，山坡上有一颗大树AB与水平面EF垂直，海啸过后，大树被刮倾斜后折断倒在山坡上，树的顶部D恰好接触到坡面AE．已知山坡的坡角∠AEF=24°，测得树干的倾斜角∠BAC=39°，大树被折断部分CD和坡面的夹角∠ADC=60°，AD=4米．
    （1）求∠DAC的度数；
    （2）求这棵大树折断前高是多少米？（结果精确到个位）（$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7，$\sqrt{6}$≈2.4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

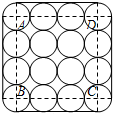    18．如图是一个组合烟花的横截面，其中16个圆的半径相同，点A、B、C、D分别是四个角上的圆的圆心，且四边形ABCD为正方形．若圆的半径为r，则组合烟花截面的周长和面积分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．当m、n是正实数，且满足m+n=mn时，我们就称点Q（m，$\frac{m}{n}$）为“完美点”
    （1）若点P（x，y）是平面内任意一个“完美点”试写出y关于x的函数解析式，并指出自变量x的取值范围．
    （2）求反比例函数y=$\frac{6}{x}$上的“完美点”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．计算：（1+$\frac{1}{2}$）（1+$\frac{1}{{2}^{2}}$）（1+$\frac{1}{{2}^{4}}$）（1+$\frac{1}{{2}^{8}}$）（1+$\frac{1}{{2}^{16}}$）=2-$\frac{1}{{2}^{31}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在表中，我们把第i行第j列的数记为ai，j（其中i，j都是不大于3的正整数），对于表中的每个数ai，j规定如下：当i≥j时，ai，j=2i-j；当i＜j时，ai，j=i+3j．例如：当i=2，j=1时，ai，j=a2，1=3，按此规定，
    （1）a1，3=10；
    （2）表中这九个数的中位数是4；
    （3）如果从表中这九个数中随机抽取一个数，那么抽到可能性最大的数是3；
    （4）如果从表中这九个数中随机抽取一个数，那么抽到素数的概率是$\frac{2}{3}$．
     a1，1 a1，2 a1，3
     a2，1 a2，2 a2，3
     a3，1 a3，2 a3，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

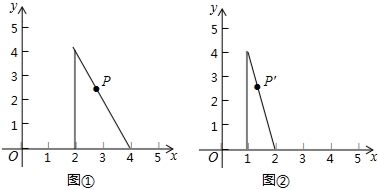
    9．点P是图①中三角形边上一点，坐标为（a，b），图①经过变化形成图②，则点P在图②中的对应点P′的坐标为（　　）
    A．（$\frac{1}{2}$a，$\frac{1}{2}$b）B．（$\frac{1}{2}$a，b）C．（a-2，b）D．（a-1，b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．试解答下列问题：
    （1）在图1我们称之为“8字形”，请直接写出∠A、∠B、∠C、∠D之间的数量关系：∠A+∠D=∠C+∠B；
    （2）仔细观察，在图2中“8字形”的个数是6个；
    （3）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求∠P的度数；
    （4）如果图2中∠D和∠B为任意角时，其他条件不变，试写出∠B与∠P、∠D之间数量关系2∠P=∠D+∠B．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算正确的是（　　）
    A．a2+a3=a5B．（-a3）2=a6C．3a2•2a3=6a6D．（a-b）2=a2-b2

    查看答案和解析>>

    同步练习册答案