练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．定义：在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，记作ctanα，即ctanα=$\frac{角α的邻边}{角α的对边}=\frac{AC}{BC}$，根据上述角的余切概念，则ctan30°=$\sqrt{3}$．

    分析 根据在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切，可得答案．

    解答 解：ctan30°=$\sqrt{3}$，
    故答案为：$\sqrt{3}$．

    点评 本题考查了锐角三角函数的定义，在直角三角形ABC中，锐角α的邻边与对边的比叫做角α的余切．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

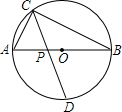    8．如图，AB是⊙O的直径，点C在⊙O上，连接AC、BC，CD平分∠ACB交⊙O于点D，若⊙O的半径是4，则$\widehat{AD}$的长度是2π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在梯形ABCD中，∠C=∠D=90°．利用面积法证明勾股定理．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．阅读下面的材料：
    解方程x4-7x2+12=0这是一个一元四次方程，根据该方程的特点，它的解法通常是：设x2=y，则x4=y2，∴原方程可化为：y2-7y+12=0，解得y1=3，y2=4，当y=3时，x2=3，x=±$\sqrt{3}$，当y=4时，x2=4，x=±2．∴原方程有四个根是：x1=$\sqrt{3}$，x2=-$\sqrt{3}$，x3=2，x4=-2，以上方法叫换元法，达到了降次的目的，体现了数学的转化思想，运用上述方法解答下列问题．
    （1）解方程：（x2+x）2-5（x2+x）+4=0；
    （2）已知实数a，b满足（a2+b2）2-3（a2+b2）-10=0，试求a2+b2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，已知三角形三个顶点的坐标分别为：A（2，-1），B（4，3），C（1，2），请你计算△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．点A、B、C在数轴上对应的数分别为1、3、5，点P在数轴上对应的数是-2，点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，…，则P1P2016的长度为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

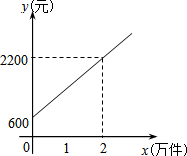    10．某公司市场营销部的营销员有部分收入按照业务量或销售额提成，即多卖多得．营销员的月提成收入y（元）与其每月的销售量x（万件）成一次函数关系，其图象如图所示．根据图象提供的信息，解答下列问题：
    （1）求出y（元）与x（万件）（其中x≥0）之间的函数关系式；
    （2）已知该公司营销员李平12月份的销售量为1.2万件，求李平12月份的提成收入．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知线段AB=3cm，延长线段AB到点C，使得BC=7cm，点D为AB的中点，则线段DC的长为8.5cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列命题是真命题的是（　　）
    A．相等的角是对顶角B．全等三角形的对应角相等
    C．如果x2=1那么x=1D．$\sqrt{4}$是无理数

    查看答案和解析>>

    同步练习册答案