
 用一块直径为4米的圆桌布平铺在对角线长为8米的正六边形桌面上(如图),若四周下垂的最大长度相等,则这个最大长度x为2-$\sqrt{3}$米.
用一块直径为4米的圆桌布平铺在对角线长为8米的正六边形桌面上(如图),若四周下垂的最大长度相等,则这个最大长度x为2-$\sqrt{3}$米. 科目:初中数学 来源: 题型:填空题
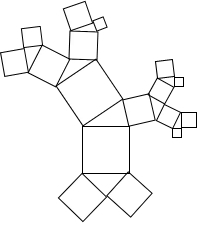 如图,美丽的珊瑚礁图案中,所有的四边形都是正方形,所有的三角形都是直角三角形.所有正方形(包括最大的正方形)的面积之和为500cm2,最大的正方形边长为10.
如图,美丽的珊瑚礁图案中,所有的四边形都是正方形,所有的三角形都是直角三角形.所有正方形(包括最大的正方形)的面积之和为500cm2,最大的正方形边长为10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一个由50个偶数排成的数阵,请你观察框内的四个数之间的关系并解答下列问题:在数阵中任意作一个类似图中的框.
已知一个由50个偶数排成的数阵,请你观察框内的四个数之间的关系并解答下列问题:在数阵中任意作一个类似图中的框.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:
为纪念爱国诗人屈原,我市在俯南河隆重举行了一次龙舟比赛,如图是甲、乙两支龙舟队在比赛时的路程s(米)与时间t(分钟)之间的图象,请你根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com