Question

【题目】（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图①，已知：在△ABC中，∠BAC=90°AB=AC，直线l经过点A，BD⊥直线L，CE⊥直线L，垂足分别为点D、E．证明：①△ABD≌△CAE；②DE=BD+CE。

（2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线L上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

Answer 1

【答案】（1）见解析；（2）成立，理由见解析.

【解析】

（1）根据同角的余角相等，可推出∠ACE=∠BAD，然后用角角边证明△ABD≌△CAE，再用全等三角形对应边相等得到BD=AE，AD=CE，从而得到DE=BD+CE；

（2）利用三角形外角性质可证得∠ABD=∠CAE，然后用角角边证明△ABD≌△CAE，同理可证明DE=BD+CE.

证明：（1）∵BD⊥直线L，CE⊥直线L，

∴∠ADB=∠CEA=90°

∴∠ACE+∠EAC=90°

又∵∠BAC=90°

∴∠BAD+∠EAC=90°，

∴∠ACE=∠BAD

在△ABD和△CAE中，

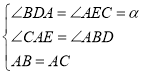
∴△ABD≌△CAE（AAS）

∴BD=AE，AD=CE

∴DE= AE+AD=BD+CE

（2）成立，理由如下：

∵∠BAE=∠BAC+∠CAE=∠ABD+∠BDA，∠BDA=∠BAC=α

∴∠CAE=∠ABD

在△ABD和△CAE中，

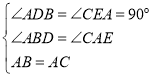
∴△ABD≌△CAE（AAS）

∴BD=AE，AD=CE

∴DE= AE+AD=BD+CE