
【题目】定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形。
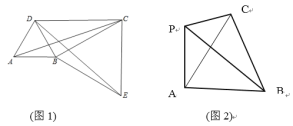
(1)如图1,将△ABC绕顶点B按顺时针方向旋转60得到△DBE,∠DCB=30,连接AD,DC,CE
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形。
(2)如图2已知等边ABC的边长等于4平面上存在一点P若使四边形PABC形成勾股四边形且PC=2,PA,PC不能同时成为一组勾股边,直接写出此时PBC的面积。
【答案】(1)见解析;(2)7.
【解析】
(1) ①由旋转的性质可知△ABC≌△DBE,从而可得BC=BE,由∠CBE=60°可得△BCE为等边三角形;②由①可得∠BCE=60°,从而可知△DCE是直角三角形,再利用勾股定理即可解决问题.
(2)根据题意可知BC和BA应组成勾股边,由此计算出PB的平方的值,过点B做PC延长线上的垂线,垂足为D,设DC=x,在△PBD中根据勾股定理可计算出x的值,即可求出BD的长度,以PC为底,BD为高即可求出PBC的面积.
(1)①∵△ABC绕点B顺时针旋转了60°到△DBE,
∴BC=BE,∠CBE=60°,
∵在△BCE中,BC=BE,∠CBE=60°
∴△BCE是等边三角形.
②∵△BCE是等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=90°,
在Rt△DCE中,有DC2+CE2=DE2,
∵DE=AC,BC=CE,
∴DC2+BC2=AC2,
∴四边形ABCD是勾股四边形.
(2)②如图,
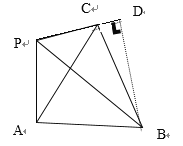
∵由条件已知PC和PA,PA和BA,PC和BC无法组成勾股边
∴若使四边形PABC形成勾股四边形
∴BC和BA应组成勾股边
∴PB2=BC2+BA2=32
如图过点B做PC延长线上的垂线,垂足为D
设CD为x,则BD2=16-x2
∵PB2=(PC+CD)2+BD2
∴32=(2+x)2+16-x2
解得x=3
∴BD=7
∴SPBC=2×7×![]() =7
=7
则PBC的面积为7.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
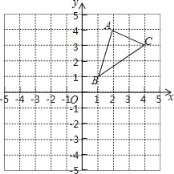
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;并写出A1、B1、C1三点的坐标.
(2)求出(1)中C点旋转到C1点所经过的路径长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
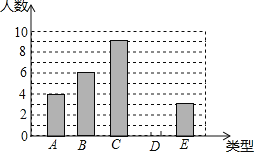
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
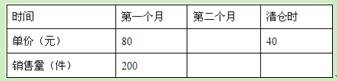
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16,AD是BC边上的中线且AD=6,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE,使点B落在点F处,连接AF,则当线段AF的长取最小值时,tan∠FBD是____.
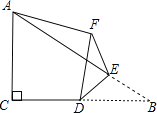
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:已知平行四边形![]() 的面积为
的面积为![]() ,
,![]() 是
是![]() 所在直线上一点.
所在直线上一点.
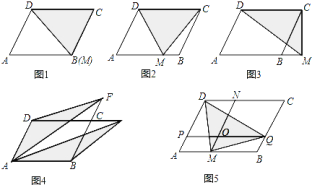
![]() 如图
如图![]() :当点
:当点![]() 与
与![]() 重合时,
重合时,![]() ________;
________;
![]() 如图
如图![]() ,当点
,当点![]() 与
与![]() 与
与![]() 均不重合时,
均不重合时,![]() ________;
________;
![]() 如图
如图![]() ,当点
,当点![]() 在
在![]() (或
(或![]() )的延长线时,
)的延长线时,![]() ________.
________.
拓展推广:如图![]() ,平行四边形
,平行四边形![]() 的面积为
的面积为![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 延长线上两点,连接
延长线上两点,连接![]() 、
、![]() 、
、![]() 、
、![]() ,求出图中阴影部分的面积,并说明理由.
,求出图中阴影部分的面积,并说明理由.
实践应用:如图是一平行四边形绿地![]() ,
,![]() 、
、![]() 分别平行于
分别平行于![]() 、
、![]() ,它们相交于点
,它们相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,现进行绿地改造,在绿地内部作一个三角形区域
,现进行绿地改造,在绿地内部作一个三角形区域![]() (连接
(连接![]() 、
、![]() 、
、![]() ,图中阴影部分)种植不同的花草,求出三角形区域的面积.
,图中阴影部分)种植不同的花草,求出三角形区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com