
【题目】已知:二次函数![]() 的图象如图所示,下列结论中:①
的图象如图所示,下列结论中:①![]() ;②
;②![]() ;③
;③![]() (
(![]() 的实数);④
的实数);④![]() ;⑤
;⑤![]() ,其中正确的是( )
,其中正确的是( )

A. 2个B. 3个C. 4个D. 1个
【答案】A
【解析】
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵抛物线的开口向上,∴a>0,
∵与y轴的交点为在y轴的负半轴上,∴c<0,
∵对称轴为![]() >0,
>0,
∴a、b异号,即b<0,
又∵c<0,∴abc>0,
故①正确;
②∵对称轴为![]() ,a>0,
,a>0,
∴0<![]() <1,
<1,
∴b<2a,
∴2a+b>0;
故②错误;
③当x=1时,y1=a+b+c;
当x=m时,y2=m(am+b)+c,当m>1,y2>y1,即可得m(am+b)>a+b,当-1<m<1,y2<y1即可得m(am+b)<a+b,所以不能确定;
故③错误;
④当x=1时,a+b+c=0;
当x=1时,ab+c>0;
∴(a+b+c)(ab+c)=0,即(a+c)2b2=0,
∴(a+c)2=b2;
故④错误;
⑤当x=1时,ab+c=2;
当x=1时,a+b+c=0,
∴a+c=1,
∴a=1+(c)>1,即a>1;
故⑤正确;
综上所述,正确的是①⑤,有2个,
故选:A.


科目:初中数学 来源: 题型:
【题目】某学校为九年级数学竞赛获奖选手购买以下三种奖品,其中小笔记本每本5元,大笔记本每本7元,钢笔每支10元,购买的大笔记本的数量是钢笔数量的2倍,共花费346元,若使购买的奖品总数最多,则这三种奖品的购买数量各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
,则称点Q为点P的“可控变点”.请问:若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,则实数a的值是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
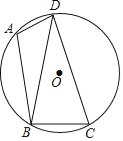
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=100°,∠DBC=80°.
(1)求证:BD=CD;
(2)若圆O的半径为9,求![]() 的长(结果保留π).
的长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACD中,∠ACD=90°,AC=b,CD=a,AD=c,点B在CD的延长线上
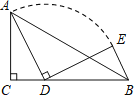
(1)求证:关于x的一元二次方程![]() 必有实数根
必有实数根
(2)当b=3,CB=5时.将线段AD绕点D顺时针旋转90°,得到线段DE,连接BE,则当a的值为多少时,线段BE的长最短,最短长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
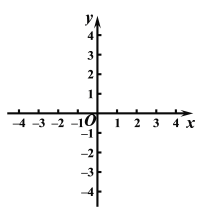
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本).
(利润=售价﹣制造成本).
(1)写出每月的利润w(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月能获得350万元的利润?
(3)当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
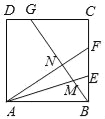
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是 .
S四边形ANGD.其中正确的结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形。
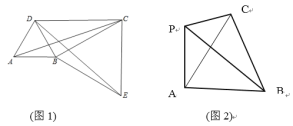
(1)如图1,将△ABC绕顶点B按顺时针方向旋转60得到△DBE,∠DCB=30,连接AD,DC,CE
①求证:△BCE是等边三角形;
②求证:四边形ABCD是勾股四边形。
(2)如图2已知等边ABC的边长等于4平面上存在一点P若使四边形PABC形成勾股四边形且PC=2,PA,PC不能同时成为一组勾股边,直接写出此时PBC的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com