
 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )
如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=20°,则∠CDE=( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
科目:初中数学 来源: 题型:解答题
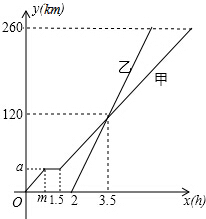 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象.请根据图象提供的信息解答下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
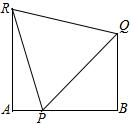 设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.
设在一条小巷内,∠A=∠B=90°,一个梯子的底脚位于点P处,当该梯子顶端靠在小巷一侧的墙上点Q时,梯子的倾斜角为45°,当顶端靠在小巷的另一侧墙上时,其顶端R离开地面高度为4米,且此时梯子的倾斜角为75°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
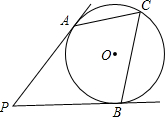 如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.
如图所示,PA,PB切⊙O于点A,B,C是$\widehat{ACB}$上的点,∠C=64°,则∠P的度数为.| A. | 26° | B. | 62° | C. | 65° | D. | 52° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinA•sinB=$\frac{CD}{AB}$ | B. | cosA=$\frac{CD}{DB}$ | C. | $\frac{CD}{sinB}$=AC | D. | BC•cosB=AD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com