
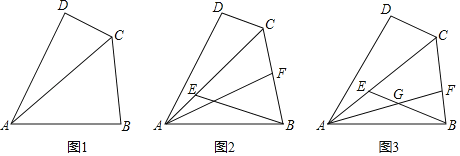
【题目】如图1,四边形ABCD中,对角线AC平分∠DCB,且AD=AB,CD<CB
(1)求证:∠B+∠D=180°;
(2)如图2,在AC上取一点E,使得BE∥CD,且BE=CE,点F在线段BC上,连接AF,且AB=AF,求证:AE=CF;
(3)如图3,在(2)的条件下,若BE与AF交于点G,BF:AB=2:7,求tan∠BGF的值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
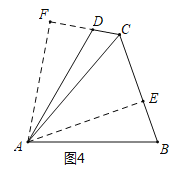
(1)如图4中,作AE⊥BC于E,作AF⊥CD交CD的延长线于F,先根据AAS证明△ACF≌△ACE,推出AF=AE,再根据HL证明Rt△AFD≌Rt△AEB,可得∠ADF=∠B,进一步即可证得结论;
(2)如图5中,作AM∥EB交CB的延长线于M,利用平行线的性质和等腰三角形的性质可证得∠CEB=∠ECB=∠EBC,则△BCE是等边三角形,进一步即可证得△ACM也是等边三角形,进而可得AE=BM,然后根据AAS可证明△ACF≌△AMB,可得CF=BM,继而可得结论;
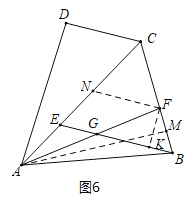
(3)如图6中,作AM⊥BC于M,FK⊥BE于K,FN∥BE交AC于N.设BF=2a,AB=7a,进而可用a的代数式依次表示出FM、BM、AM、CM,易证△CNF是等边三角形,进一步即可表示出FN、EN,易得△AEG∽△ANF,然后利用相似三角形的性质即可用含a的代数式表示出EG,进而可得GB,而在直角△BFK中,FK、BK易得,问题即得解决.
解:(1)证明:如图4中,作AE⊥BC于E,作AF⊥CD交CD的延长线于F.
∵∠AFC=∠AEC=90°,∠ACF=∠ACE,AC=AC,
∴△ACF≌△ACE(AAS),∴AF=AE,
∵AD=AB,∠F=∠AEB=90°,
∴Rt△AFD≌Rt△AEB(HL),∴∠ADF=∠B,
∵∠ADF+∠ADC=180°,∴∠ADC+∠B=180°;
(2)证明:如图5中,作AM∥EB交CB的延长线于M.
∵BE=EC,∴∠ECB=∠EBC,
∵CD∥BE,∴∠DCE=∠CEB,
∵∠DCE=∠ECB,
∴∠CEB=∠ECB=∠EBC=60°,
∴△ECB是等边三角形,
∵EB∥AM,∴∠CEB=∠CAB=60°,∠CBE=∠M=60°,
∴△ACM是等边三角形,∴CA=CM,
∵CE=CB,∴AE=BM,
∵AF=AB,∴∠AFB=∠ABF,∴∠AFC=∠ABM,
又∵AC=AM,∠ACF=∠M=60°,
∴△ACF≌△AMB(AAS),
∴CF=BM,∴AE=CF;

(3)解:如图6中,作AM⊥BC于M,FK⊥BE于K,FN∥BE交AC于N.
∵FB:AB=2:7,∴设BF=2a,AB=7a,
∵AF=AB,AM⊥BF,∴FM=BM=a,
∴AM=![]() ,
,
∵∠ACM=60°,∴AM=![]() CM,∴CM=4a,CF=AE=CM-FM=3a,
CM,∴CM=4a,CF=AE=CM-FM=3a,
∵FN∥BE,∴∠CNF=∠CEB=60°,∠CFE=∠CBE=60°,∴△CNF是等边三角形,
∴CF=CN=FN=3a,EN=BF=2a,AN=AE+EN=5a,
∵EG∥FN,∴△AEG∽△ANF,∴![]() ,即
,即![]() ,
,
∴EG=![]() a,BG=EB﹣EG=5a﹣
a,BG=EB﹣EG=5a﹣![]() a=
a=![]() a,
a,
在Rt△BFK中,∵BF=2a,∠FBK=60°,∴BK=a,FK=![]() a,
a,
∴GK=BG﹣BK=![]() a﹣a=
a﹣a=![]() a,
a,
∴tan∠FGB=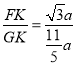 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】有2个信封,每个信封内各装有四张卡片,其中一个信封内的三张卡片上分别写有1、2、3、三个数,另一个信封内的三张卡片分别写有4、5、6三个数,甲、乙两人商定了一个游戏,规则是:从这两个信封中各随机抽取一张卡片,然后把卡片上的两个数相乘,如果得到的积大于10,则甲获胜,否则乙获胜.
(1)请你通过列表(或画树状图)计算甲获胜的概率.
(2)你认为这个游戏公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毕业在即,重庆实验外国语学校初2016级拍摄了毕业照,每个班都得到了若干张风格迥异的照片样品供同学们选择.年级团委书记王老师想了解同学们对照片的选择情况,在全年级进行了一次抽样调查,按照同学们选择的张数把选择情况分为四个层次: A:4张;B:3张;C:2张;D:1张.并将调查结果绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
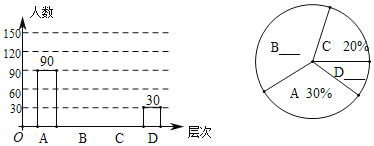
请你根据图中提供的信息解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)根据调查结果,估计初2016级2000名同学一共选择了多少张毕业照?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D为AC中点,点E在BD延长线上,且BD:DE=3:5,连接CE,tan∠BAC=![]() ,CB=
,CB=![]() ,则线段EC长为_____.
,则线段EC长为_____.
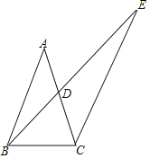
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 内接于
内接于![]() ,且
,且![]() 为
为![]() 的直径.
的直径.![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
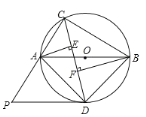
(1)求证:![]() ;
;
(2)试猜想线段![]() ,
,![]() ,
,![]() 之间有何数量关系,并加以证明;
之间有何数量关系,并加以证明;
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(﹣9,0),B(0,6)两点,过点C(2,0)作直线l与BC垂直,点E在直线l位于x轴上方的部分.
(1)求一次函数y=kx+b(k≠0)的表达式;
(2)若△ACE的面积为11,求点E的坐标;
(3)当∠CBE=∠ABO时,点E的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
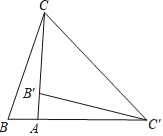
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于点A(2,a).
交于点A(2,a).
(1)求![]() 与
与![]() 的值;
的值;
(2)画出双曲线![]() 的示意图;
的示意图;
(3)设点![]() 是双曲线
是双曲线![]() 上一点(
上一点(![]() 与
与![]() 不重合),直线
不重合),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,结合图象,直接写出
时,结合图象,直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com