
【题目】毕业在即,重庆实验外国语学校初2016级拍摄了毕业照,每个班都得到了若干张风格迥异的照片样品供同学们选择.年级团委书记王老师想了解同学们对照片的选择情况,在全年级进行了一次抽样调查,按照同学们选择的张数把选择情况分为四个层次: A:4张;B:3张;C:2张;D:1张.并将调查结果绘制成以下条形统计图和扇形统计图,请你结合图中信息解答下列问题:
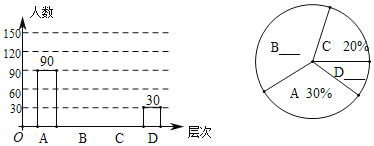
请你根据图中提供的信息解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)根据调查结果,估计初2016级2000名同学一共选择了多少张毕业照?
【答案】(1)详见解析;(2)5800
【解析】
(1)先由A层次人数及其所占百分比求出总人数,总人数乘以C层次百分比求出其人数,D层次人数除以总人数可得其所占百分比,继而根据各层次人数之和等于总人数,百分比之和为1求解可得;
(2)先求出样本中300人拍摄照片张数的平均数,再乘以总人数即可得.
解:(1)∵被调查的总人数为90÷30%=300(人),
∴C层次人数为300×20%=60(人),D层次对应的百分比为![]() ×100%=10%,
×100%=10%,
则B层次人数为300﹣(90+60+30)=120(人),B层次对应的百分比为1﹣(30%+20%+10%)=40%,
补全图形如下:
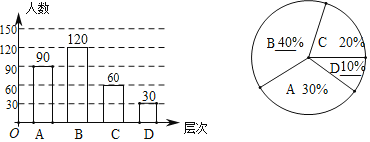
(2)∵![]() (张/人),
(张/人),
∴2000×2.9=5800(张).
∴估计初2016级2000名同学一共选择了5800张毕业照.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,OA=3,OC=4,P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90交直线BC于点Q.
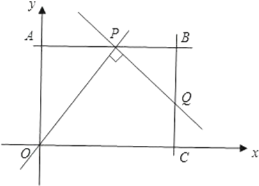
(1)当点P在线段AB上运动(不与A,B重合)时,求证:OABQ=APBP;
(2)在(1)成立的条件下,设点P的横坐标为m,线段CQ的长度为![]() ,求出
,求出![]() 关于m的函数解析式,并判断
关于m的函数解析式,并判断![]() 是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)直线AB上是否存在点P,使△POQ为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
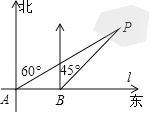
查看答案和解析>>
科目:初中数学 来源: 题型:
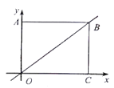
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 分别在坐标轴的正半轴上,
分别在坐标轴的正半轴上, ![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与折线
与折线![]() 有公共点.
有公共点.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)对于一次函数![]() ,当
,当![]() 随
随![]() 的增大而减小时,直接写出
的增大而减小时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y1=x2+bx+c与直线y2=2x+m相交于A(1,4)、B(﹣1,n)两点.
(1)求y1和y2的解析式;
(2)直接写出y1﹣y2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
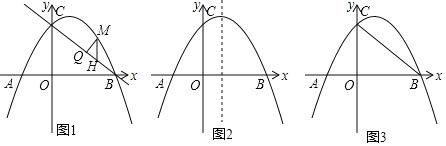
【题目】如图1,已知抛物线y=﹣![]() x+3与x轴交于A和B两点,(点A在点B的左侧),与y轴交于点C.
x+3与x轴交于A和B两点,(点A在点B的左侧),与y轴交于点C.
(1)求出直线BC的解析式.
(2)M为线段BC上方抛物线上一动点,过M作x轴的垂线交BC于H,过M作MQ⊥BC于Q,求出△MHQ周长最大值并求出此时M的坐标;当△MHQ的周长最大时在对称轴上找一点R,使|AR﹣MR|最大,求出此时R的坐标.
(3)T为线段BC上一动点,将△OCT沿边OT翻折得到△OC′T,是否存在点T使△OC′T与△OBC的重叠部分为直角三角形,若存在请求出BT的长,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点
的图象过点![]() .
.
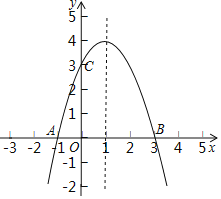
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由;
(3)在(2)的条件下,在x轴上方的抛物线上是否存在点M(不与C点重合),使得![]() ?若存在,请求出点M的坐标;若不存在,请说明理由.
?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
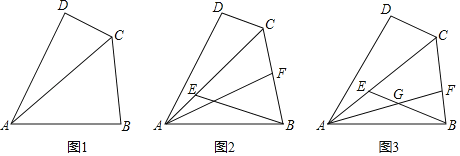
【题目】如图1,四边形ABCD中,对角线AC平分∠DCB,且AD=AB,CD<CB
(1)求证:∠B+∠D=180°;
(2)如图2,在AC上取一点E,使得BE∥CD,且BE=CE,点F在线段BC上,连接AF,且AB=AF,求证:AE=CF;
(3)如图3,在(2)的条件下,若BE与AF交于点G,BF:AB=2:7,求tan∠BGF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
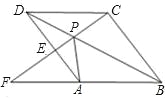
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com