
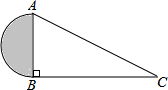
 如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?
如图,∠ABC=90°,CB=15,AC=17,则阴影部分面积是多少?  黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
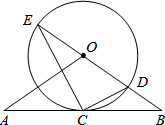 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
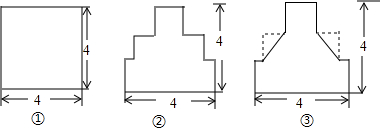
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
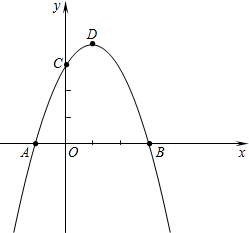 如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0)、点B(3,0)、点C(0,3).
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0)、点B(3,0)、点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
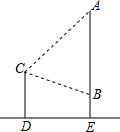 如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)
如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
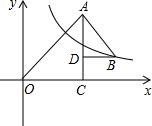 如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )| A. | 12 | B. | 9 | C. | 8 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com