
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(4,1)与点B(0,5). 
(1)求一次函数的表达式;
(2)若P点为此一次函数图象上一点,且S△POB= ![]() S△AOB , 求P点的坐标.
S△AOB , 求P点的坐标.
【答案】
(1)解:设一次函数的解析式为y=kx+b,
将A(4,1)、B(0,5)代入得: ![]() ,
,
解得: ![]() ,
,
∴一次函数表达式为y=﹣x+5
(2)解:设P(x,﹣x+5),
∵S△POB= ![]() S△AOB,
S△AOB,
∴ ![]() ×OB|xP|=
×OB|xP|= ![]() ×OBxA,即
×OBxA,即 ![]() ×5|xP|=
×5|xP|= ![]() ×
× ![]() ×5×4,
×5×4,
解得:xP=6或xP=﹣6,
∴点P的坐标为(6,﹣1)或(﹣6,11)
【解析】(1)待定系数法求解可得;(2)设P(x,﹣x+5),根据S△POB= ![]() S△AOB可得
S△AOB可得 ![]() ×OB|xP|=
×OB|xP|= ![]() ×OBxA , 即
×OBxA , 即 ![]() ×5|xP|=
×5|xP|= ![]() ×
× ![]() ×5×4,解之求得xP即可知答案.
×5×4,解之求得xP即可知答案.
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


科目:初中数学 来源: 题型:
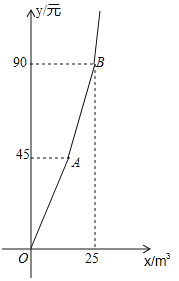
【题目】为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系.
(1)写出点B的实际意义;
(2)求线段AB所在直线的表达式;
(3)某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(2,2),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,连接CD,直线CD与直线y=x交于点Q,当△OPC≌△ADP时,则C点的坐标是 , Q点的坐标是 . 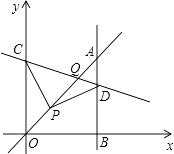
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,小明骑自行车从家里出发到野外郊游,从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地,小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍. 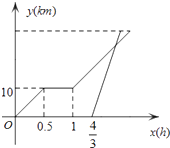
(1)直接写出小明开始骑车的0.5小时内所对应的函数解析式 .
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早12分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
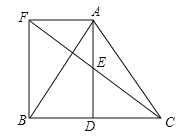
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com