
【题目】阅读材料:若![]() ,求
,求![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .
.
根据你的观察,探究下面的问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知△ABC的三边长![]() ,且满足
,且满足![]() ,求c的取值范围;
,求c的取值范围;
(3)已知![]() ,
,![]() ,比较
,比较![]() 的大小.
的大小.
【答案】(1)xy的值是9;(2)1<c<11;(3)P>Q.
【解析】
(1)根据x2-2xy+2y2+6y+9=0,先仿照例子得出(x-y)2+(y+3)2=0,求出x、y的值,从而得出结果;
(2)首先根据a2+b2-10a-12b+61=0,先得出(a-5)2+(b-6)2=0,求出a、b的值,然后根据三角形的三条关系,可求出c的取值范围;
(3)利用作差法,得出P-Q=x2-6x+y2+4y+14=(x-3)2+(y+2)2+1>0,从而可得出结果.
解:(1)∵x2-2xy+2y2+6y+9=0,
∴(x2-2xy+y2)+(y2+6y+9)=0,
∴(x-y)2+(y+3)2=0,
∴x-y=0,y+3=0,
∴x=-3,y=-3,
∴xy=(-3)×(-3)=9,
即xy的值是9;
(2)∵a2+b2-10a-12b+61=0,
∴(a2-10a+25)+(b2-12b+36)=0,
∴(a-5)2+(b-6)2=0,
∴a-5=0,b-6=0,
∴a=5,b=6,
根据三角形的三边关系可得,6-5<c<6+5,
∴1<c<11;
(3)P-Q=x2-6x+y2+4y+14=(x-3)2+(y+2)2+1>0,
∴P>Q.


科目:初中数学 来源: 题型:
【题目】某次篮球联赛初赛阶段,每队有![]() 场比赛,每场比赛都要分出胜负,每队胜一场得
场比赛,每场比赛都要分出胜负,每队胜一场得![]() 分, 负一场得
分, 负一场得![]() 分,积分超过
分,积分超过![]() 分才能获得参赛资格.
分才能获得参赛资格.
(1)已知甲队在初赛阶段的积分为![]() 分,求甲队初赛阶段胜、负各多少场;
分,求甲队初赛阶段胜、负各多少场;
(2)如果乙队要获得参加决赛资格,那么乙队在初赛阶段至少要胜多少场?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .一次函数的图象分别交
.一次函数的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
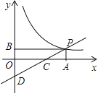
(1)求点![]() 的坐标;
的坐标;
(2)求一次函数与反比例函数的解析式:
(3)根据图象写出当![]() 时,一次函数的值小于反比例函数的值的
时,一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
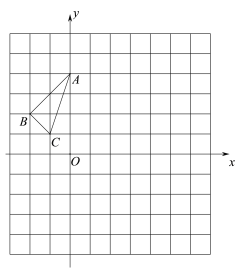
【题目】△ABC在平面直角坐标系中的位置如图所示,其中A(0,4),B(-2,2),C((-1,1),先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称.
(1)画出△A1B1C1和△A2B2C2,并写出A2,B2,C2的坐标;
(2)在x轴上确定一点P,使BP+A1P的值最小,请在图中画出点P;
(3)点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
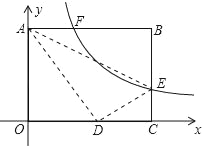
【题目】如图,矩形ABCO的顶点B(10,8),点A,C在坐标轴上,E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段BF的长为_____.
的图象与边AB交于点F,则线段BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.
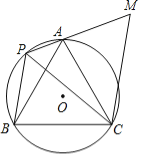
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2,求△PCM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com