
【题目】△ABC在平面直角坐标系中的位置如图所示,其中A(0,4),B(-2,2),C((-1,1),先将△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称.
(1)画出△A1B1C1和△A2B2C2,并写出A2,B2,C2的坐标;
(2)在x轴上确定一点P,使BP+A1P的值最小,请在图中画出点P;
(3)点Q在y轴上且满足△ACQ为等腰三角形,则这样的Q点有 个.
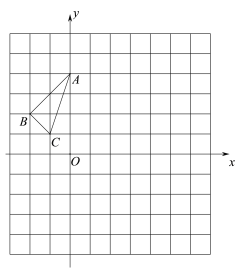
【答案】(1)作图见解析,A2,B2,C2的坐标分别为A2(3,-3),B2(1,-1),C2(2,0);(2)见解析;(3)4.
【解析】
(1)△ABC向右平移3个单位,再向下平移1个单位到△A1B1C1,△A1B1C1和△A2B2C2关于x轴对称,根据平移的性质和轴对称的性质先找出对应顶点的坐标,顺次连接即可;
(2)依据轴对称的性质,连接BA2,交x轴于点P,此时BP+A1P的值最小;
(3)在平面直角坐标系中,作线段AC的垂直平分线,与y轴有1个交点,分别以A,C为圆心,AC长为半径画弧,与y轴的交点有3个,即可得到Q点的数量.
解:(1)如图所示,△A1B1C1和△A2B2C2即为所求,
根据图形可得,A2,B2,C2的坐标分别为A2(3,-3),B2(1,-1),C2(2,0);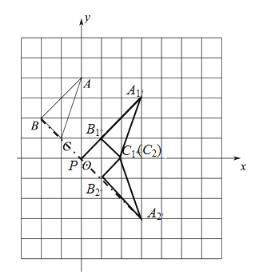
(2)如图所示,连接BA2,交x轴于点P,则点P即为所求;
(3)根据点Q在y轴上且满足△ACQ为等腰三角形,在平面直角坐标系中,作线段AC的垂直平分线,与y轴有1个交点,分别以A,C为圆心,AC长为半径画弧,与y轴的交点有3个,可得这样的Q点有4个.
故答案为:4.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿折线
的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒.
秒.


备用图
(1)![]() ___________
___________![]() ;
;
(2)若点![]() 恰好在
恰好在![]() 的角平分线上,求此时
的角平分线上,求此时![]() 的值:
的值:
(3)在运动过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月12日是母亲节,小明去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支5元,兰花每支3元,小明只有30元,希望购买花的支数不少于7支,其中至少有一支是康乃馨.
(1)小明一共有多少种可能的购买方案?列出所有方案;
(2)如果小明先购买一张2元的祝福卡,再从(1)中任选一种方案购花,求他能实现购买愿望的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第一、三象限内的
的图象交于第一、三象限内的![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
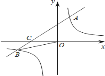
(1)求该反比例函数和一次函数的解析式,并写出使![]() 成立的
成立的![]() 的取值范围;
的取值范围;
(2)若![]() 是直线
是直线![]() 上一点,使得
上一点,使得![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
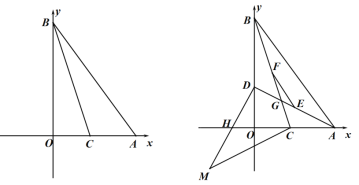
【题目】如图,在平面直角坐标系中,O为坐标原点,A点的坐标为(18,0),B点的坐标为(0,24).
(1)求AB的值;
(2)点C在OA上,且BC平分∠OBA,求点C的坐标;
(3)在(2)的条件下,点M在第三象限,点D为y轴上的一个点,连接DM交x轴于点H,连接CM,点F为BC的中点,点E为AD的中点,AD与BC交于点G,,点H为DM的中点,当∠MCG-∠DGF=∠OAB,且AD=CM时,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求
,求![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .
.
根据你的观察,探究下面的问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知△ABC的三边长![]() ,且满足
,且满足![]() ,求c的取值范围;
,求c的取值范围;
(3)已知![]() ,
,![]() ,比较
,比较![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
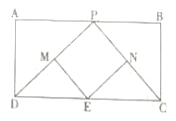
【题目】如图,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,
上一动点,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形,说明理由.
是菱形,说明理由.
(3)四边形![]() 有可能是矩形吗?若有可能,求出
有可能是矩形吗?若有可能,求出![]() 的长;若不可能,请说明理由.
的长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
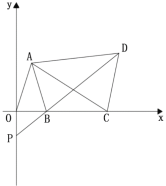
【题目】如图,平面直角坐标系中,已知点![]() 且
且![]() 为
为![]() 轴上点
轴上点![]() 右侧的动点,以
右侧的动点,以![]() 为腰作等腰
为腰作等腰![]() ,使
,使![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点![]() 运动时,点
运动时,点![]() 在
在![]() 轴上的位置是否发生改变,为什么?
轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
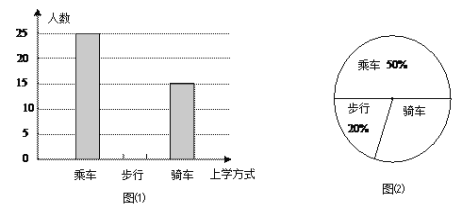
【题目】学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)求该班共有多少名学生;
(2)在图(1)中,将表示“步行”的部分补充完整;
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数;
(4)如果全年级共600名同学,请你估算全年级步行上学的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com