
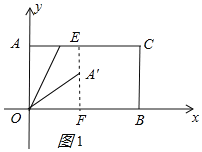
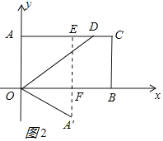
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应点为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为__.
【答案】(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2)
,﹣2)
【解析】
由已知得出∠A=90°,BC=OA=4,OB=AC=7,分两种情况:
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,当A'E:A'F=1:3时,求出A'E=1,A'F=3,由折叠的性质得:OA'=OA=4,∠OA'D=∠A=90°,在Rt△OA'F中,由勾股定理求出OF=![]() ,即可得出答案;
,即可得出答案;
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,由A'F:A'E=1:3,则A'F:EF=1:2,求出A'F=![]() EF=
EF=![]() BC=2,在Rt△OA'F中,由勾股定理求出OF=2
BC=2,在Rt△OA'F中,由勾股定理求出OF=2![]() ,即可得出答案.
,即可得出答案.
解:∵点A(0,4),B(7,0),C(7,4),
∴BC=OA=4,OB=AC=7,
分两种情况:
(1)当点A'在矩形AOBC的内部时,过A'作OB的垂线交OB于F,交AC于E,如图1所示:
①当A'E:A'F=1:3时,
∵A'E+A'F=BC=4,
∴A'E=1,A'F=3,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() ,
,
∴A'(![]() ,3);
,3);
②当A'E:A'F=3:1时,同理得:A'(![]() ,1);
,1);
(2)当点A'在矩形AOBC的外部时,此时点A'在第四象限,过A'作OB的垂线交OB于F,交AC于E,如图2所示:∵A'F:A'E=1:3,则A'F:EF=1:2,
∴A'F=![]() EF=
EF=![]() BC=2,
BC=2,
由折叠的性质得:OA'=OA=4,
在Rt△OA'F中,由勾股定理得:OF=![]() =2
=2![]() ,
,
∴A'(2![]() ,﹣2);
,﹣2);
故答案为:(![]() ,3)或(
,3)或(![]() ,1)或(2
,1)或(2![]() ,﹣2).
,﹣2).


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是圆上一点,弦
是圆上一点,弦![]() 于点
于点![]() ,且
,且![]() .过点
.过点![]() 作
作![]() 的切线,过点
的切线,过点![]() 作
作![]() 的平行线,两直线交于点
的平行线,两直线交于点![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() .
.
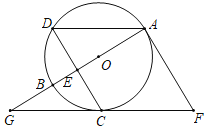
(1)求证:![]() 与
与![]() 相切;
相切;
(2)连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=4cm,AC为对角线,AC上有一动点P,M是AB边的中点,连接PM、PB,设A、P两点间的距离为xcm,PM+PB长度为ycm.
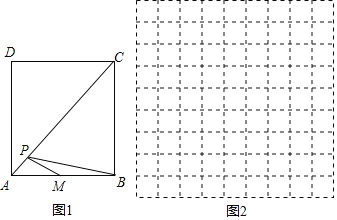
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 6.0 | 4.8 | 4.5 | 6.0 | 7.4 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:PM+PB的长度最小值约为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP=5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在凸四边形ABCD中,AB=BC=CD,∠ABC+∠BCD=240°.设∠ABC=α.
(1)利用尺规,以CD为边在四边形内部作等边△CDE.(保留作图痕迹,不需要写作法)
(2)连接AE,判断四边形ABCE的形状,并说明理由.
(3)求证:∠ADC=![]() α;
α;
(4)若CD=6,取CD的中点F,连结AF,当∠ABC等于多少度时,AF最大,最大值为多少.(直接写出答案,不需要说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
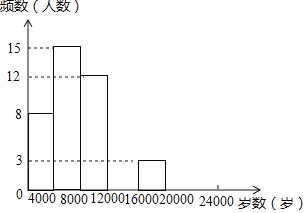
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量山坡上的电线杆PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为30°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是60°,求信号塔PQ得高度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高,空气净化器成为很多家庭的新电器.某品牌的空气净化器厂家为进一步了解市场,制定生产计划,根据2016年下半年销售情况绘制了如下统计图,其中同比增长率=(![]() ﹣1)×100%,下面有四个推断:
﹣1)×100%,下面有四个推断:
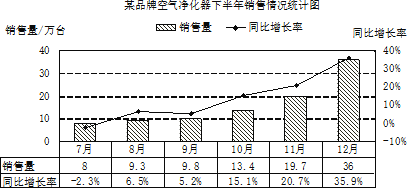
①2016年下半年各月销售量均比2015年同月销售量增多
②第四季度销售量占下半年销售量的七成以上
③下半年月均销售量约为16万台
④下半年月销售量的中位数不超过10万台
其中合理的是( )
A.①②B.①④C.②③D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com