
【题目】在正方形ABCD中,AB=4cm,AC为对角线,AC上有一动点P,M是AB边的中点,连接PM、PB,设A、P两点间的距离为xcm,PM+PB长度为ycm.
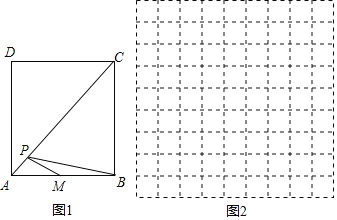
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 6.0 | 4.8 | 4.5 | 6.0 | 7.4 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:PM+PB的长度最小值约为______cm.
【答案】(1)5.0;(2)见解析;(3)x=2时,函数有最小值y=4.5
【解析】
(1)通过作辅助线,应用三角函数可求得HM+HN的值即为x=2时,y的值;
(2)可在网格图中直接画出函数图象;
(3)由函数图象可知函数的最小值.
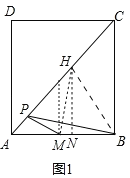
(1)当点P运动到点H时,AH=3,作HN⊥AB于点N.
∵在正方形ABCD中,AB=4cm,AC为对角线,AC上有一动点P,M是AB边的中点,∴∠HAN=45°,∴AN=HN=AHsin45°=3![]() ,∴HM
,∴HM![]() ,HB
,HB![]() ,∴HM+HN=
,∴HM+HN=![]() =
=![]() ≈
≈![]() ≈2.125+2.834≈5.0.
≈2.125+2.834≈5.0.
故答案为:5.0;
(2)
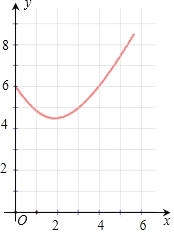
(3)根据函数图象可知,当x=2时,函数有最小值y=4.5.
故答案为:4.5.


科目:初中数学 来源: 题型:
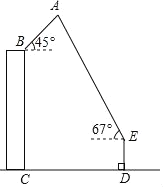
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况.2019年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度(单位:微粒/立方米)表
浓度(单位:微粒/立方米)表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 33 | 海淀 | 50 | 平谷 | 45 |
密云 | 34 | 延庆 | 51 | 丰台 | 61 |
门头沟 | 41 | 西城 | 61 | 大兴 | 72 |
顺义 | 41 | 东城 | 60 | 开发区 | 65 |
昌平 | 38 | 石景山 | 55 | 房山 | 62 |
朝阳 | 54 | 通州 | 57 |
从上述表格随机选择一个区域,其2019年1月份![]() 的浓度小于51微克/立方米的概率是______.
的浓度小于51微克/立方米的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,
,![]() ,给出如下定义:若
,给出如下定义:若![]() ,
,![]() 为某个三角形的顶点,且边
为某个三角形的顶点,且边![]() 上的高
上的高![]() ,满足
,满足![]() ,则称该三角形为点
,则称该三角形为点![]() ,
,![]() 的“生成三角形”.
的“生成三角形”.
(1)已知点![]() ;
;
①若以线段![]() 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点![]() ,
,![]() 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;
②若![]() 是点
是点![]() ,
,![]() 的“生成三角形”,且点
的“生成三角形”,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的坐标为______;
的坐标为______;
(2)![]() 的圆心为点
的圆心为点![]() ,半径为2,点
,半径为2,点![]() 的坐标为
的坐标为![]() ,
,![]() 为直线
为直线![]() 上一点,若存在
上一点,若存在![]() ,是点
,是点![]() ,
,![]() 的“生成三角形”,且边
的“生成三角形”,且边![]() 与
与![]() 有公共点,直接写出点
有公共点,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.
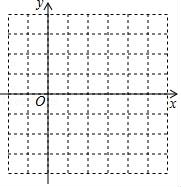
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为正六边形对角线的交点,机器人置于该正六边形的某顶点处,柱柱同学操控机器人以每秒1个单位长度的速度在图1中给出线段路径上运行,柱柱同学将机器人运行时间设为t秒,机器人到点A的距离设为y,得到函数图象如图2,通过观察函数图象,可以得到下列推断:①该正六边形的边长为1;②当t=3时,机器人一定位于点O;③机器人一定经过点D;④机器人一定经过点E;其中正确的有( )
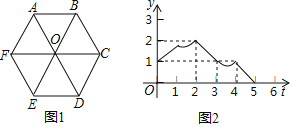
A.①④B.①③C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
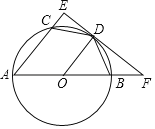
【题目】如图,已知AB为⊙O的直径,AC是⊙O的弦,D是弧BC的中点,过点D作⊙O的切线,分别交AC、AB的延长线于点E和点F,连接CD、BD.
(1)求证:∠A=2∠BDF;
(2)若AC=3,AB=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,4),B(7,0),C(7,4),连接AC,BC得到矩形AOBC,点D的边AC上,将边OA沿OD折叠,点A的对应点为A'.若点A'到矩形较长两对边的距离之比为1:3,则点A'的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+ax+2a+1的图象经过点M(2,-3)。
(1)求二次函数的表达式;
(2)若一次函数y=kx+b(k≠0)的图象与二次函数y=x2+ax+2a+1的图象经过x轴上同一点,探究实数k,b满足的关系式;
(3)将二次函数y=x2+ax+2a+1的图象向右平移2个单位,若点P(x0,m)和Q(2,n)在平移后的图象上,且m>n,结合图象求x0的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com