
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
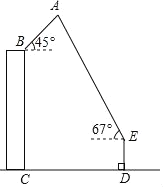
【答案】风筝距地面的高度49.9m.
【解析】
作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.设AF=BF=x,则CM=BF=x,DM=HE=40-x,AH=x+30-1.5=x+28.5, 在Rt△AHE中,利用∠AEH的正切列方程求解即可.
如图,作AM⊥CD于M,作BF⊥AM于F,EH⊥AM于H.
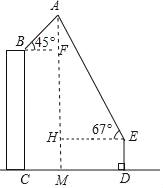
∵∠ABF=45°,∠AFB=90°,
∴AF=BF,设AF=BF=x,则CM=BF=x,DM=HE=40-x,AH=x+30-1.5=x+28.5,
在Rt△AHE中,tan67°=![]() ,
,
∴![]() ,
,
解得x≈19.9 m.
∴AM=19.9+30=49.9 m.
∴风筝距地面的高度49.9 m.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
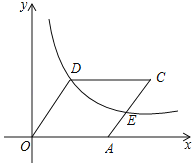
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
(k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
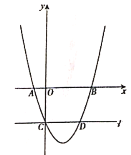
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该抛物线交于另一点
与该抛物线交于另一点![]() ,并且直线
,并且直线![]() 轴,点
轴,点![]() 为该抛物线上一个动点,点
为该抛物线上一个动点,点![]() 为直线
为直线![]() 上一个动点.
上一个动点.
(1)当![]() ,且
,且![]() 时,连接
时,连接![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是平行四边形
是平行四边形
(2)当![]() 时,连接
时,连接![]() ,线段
,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)连接![]() ,
,![]() ,试探究:是否存在点
,试探究:是否存在点![]() ,使得
,使得![]() 与
与![]() 互为余角?若存在,求出点
互为余角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的网格(每个小正方形的边长为1)在平面直角坐标系
的网格(每个小正方形的边长为1)在平面直角坐标系![]() 中,其两边恰在坐标轴上,若反比例函数
中,其两边恰在坐标轴上,若反比例函数![]() (
(![]() )的图象与一次函数的图象恰好都经过其中的两个相同的网格点.
)的图象与一次函数的图象恰好都经过其中的两个相同的网格点.
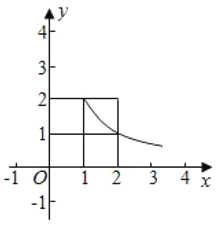
(1)求k的值:
(2)求一次函数的解析式;
(3)设点![]() ,过点A的直线l与y轴交于点B,若在
,过点A的直线l与y轴交于点B,若在![]() (
(![]() )的图象上存在点C,使得
)的图象上存在点C,使得![]() ,结合图象,直接写出点B纵坐标的取值范围.
,结合图象,直接写出点B纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为![]() 的
的![]() 多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒
多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒![]() 米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
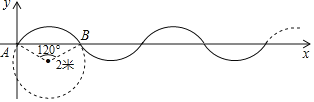
A. ﹣2B. ﹣1C. 0D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张三角形纸片![]() ,其三边之比为
,其三边之比为![]() .小方将纸片对折,第一次使顶点
.小方将纸片对折,第一次使顶点![]() 和
和![]() 重合,第二次使顶点
重合,第二次使顶点![]() 和
和![]() 重合,第三次使顶点
重合,第三次使顶点![]() 和
和![]() 重合,三条折痕依次记为
重合,三条折痕依次记为![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
查看答案和解析>>
科目:初中数学 来源: 题型:
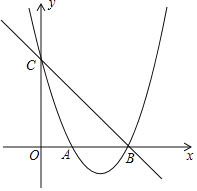
【题目】如图,已知二次函数y=ax2+bx+3的图象交x轴于点A(1,0),B(3,0),交y轴于点C.
(1)求这个二次函数的表达式;
(2)点P是直线BC下方抛物线上的一动点,求△BCP面积的最大值;
(3)直线x=m分别交直线BC和抛物线于点M,N,当△BMN是等腰三角形时,直接写出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com