
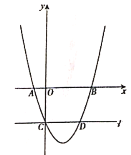
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该抛物线交于另一点
与该抛物线交于另一点![]() ,并且直线
,并且直线![]() 轴,点
轴,点![]() 为该抛物线上一个动点,点
为该抛物线上一个动点,点![]() 为直线
为直线![]() 上一个动点.
上一个动点.
(1)当![]() ,且
,且![]() 时,连接
时,连接![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是平行四边形
是平行四边形
(2)当![]() 时,连接
时,连接![]() ,线段
,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)连接![]() ,
,![]() ,试探究:是否存在点
,试探究:是否存在点![]() ,使得
,使得![]() 与
与![]() 互为余角?若存在,求出点
互为余角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由二次函数的性质,先求出点A、B、C的坐标,然后得到点D的坐标,则得到![]() 与
与![]() 的值,把点P代入抛物线,求出m的值,由平行四边形的判定,即可得到答案;
的值,把点P代入抛物线,求出m的值,由平行四边形的判定,即可得到答案;
(2)由题意,表示PQ的长度,然后求出![]() ,
,![]() ,再由
,再由![]() ,得到
,得到![]() ,即可得到答案;
,即可得到答案;
(3)根据题意,利用三角函数得到![]() ,然后分两种情况进行分类讨论:①当点
,然后分两种情况进行分类讨论:①当点![]() 在直线
在直线![]() 上方时,
上方时,![]() ;②当点
;②当点![]() 在直线
在直线![]() 下方时,
下方时,![]() ,
,
![]() ;分别求出m的值,即可得到点P的坐标.
;分别求出m的值,即可得到点P的坐标.
解:如图:
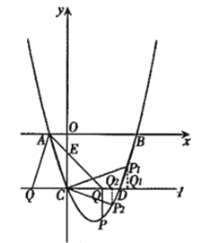
(1)证明:当![]() 时,
时,![]() ,
,
解得![]() ,
,
![]() ,
,
![]() .
.
当![]() 时,
时,![]() ,
,
![]() .
.
∵直线![]() 轴,
轴,
∴直线![]() 的解析式为
的解析式为![]() .
.
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() .
.
∵点![]() 在直线
在直线![]() 上,
上,
![]() .
.
![]()
![]() ,
,
![]() ,点
,点![]() 在该抛物线上,
在该抛物线上,
![]()
解得![]() 或
或![]() (舍去).
(舍去).
∵直线![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
(2)![]() 两点的横坐标都是
两点的横坐标都是![]() ,
,
∴直线![]() 轴,
轴,
![]()
设![]() ,则
,则![]() ,
,
![]() ,
,
解得:![]() 或
或![]() .
.
![]() ,
,
![]() ,
,![]() .
.
∵直线![]() 轴,
轴,
![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)假设存在点![]() ,使得
,使得![]() 与
与![]() 互为余角,即
互为余角,即![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]()
连接![]() .
.
∵直线![]() 轴,直线
轴,直线![]() 轴,
轴,
![]() 是直角三角形,且
是直角三角形,且![]() .
.
![]()
①当点![]() 在直线
在直线![]() 上方时,
上方时,![]()
(i)若点![]() 在
在![]() 轴左侧,则
轴左侧,则![]() ,
,
![]() .
.
![]() ,解得
,解得![]() (舍去),
(舍去),![]() (舍去).
(舍去).
(ii)若点![]() 在
在![]() 轴右侧,则
轴右侧,则![]() ,
,
![]() .
.
![]() ,解得
,解得![]() (舍去),
(舍去),![]() .
.
![]()
![]() ,
,
![]()
②当点![]() 在直线
在直线![]() 下方时,
下方时,![]() ,
,
![]()
![]() ,解得
,解得![]() (舍去),
(舍去),![]()
![]()
![]() ,
,
![]() ;
;
综上,存在点![]() ,使得
,使得![]() 与
与![]() 互为余角.
互为余角.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】有一个著名的希波克拉蒂月牙问题:如图1,以直角三角形的各边为直径分别向上作半圆,则直角三角形的面积可表示成两个月牙形的面积之和,现将三个半圆纸片沿直角三角形的各边向下翻折得到图2,把较小的两张半圆纸片的重叠部分面积记为S1,大半圆纸片未被覆盖部分的面积记为S2,则直角三角形的面积可表示成( )
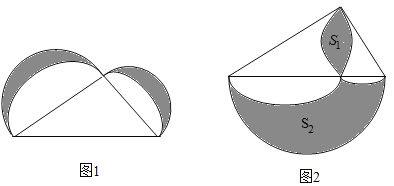
A.S1+S2B.S2﹣S1C.S2﹣2S1D.S1S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.

(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年的寒假是“不同寻常”的一个假期.在这个超长假期里,某中学随机对本校部分同学进行“抗疫有我,在家可以这么做”的问卷调查:A扎实学习、B经典阅读、C分担劳动、D乐享健康,(每位同学只能选一个),并根据调查结果绘制如下两幅不完整的统计图.
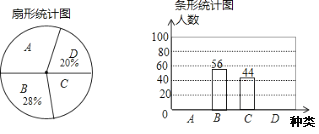
根据统计图提供信息,解答问题:
(1)本次一共调查了_______名同学;
(2)请补全条形统计图;在扇形统计图中A所对应的圆心角为 度;
(3)若该校共有1600名同学,请你估计选择A有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
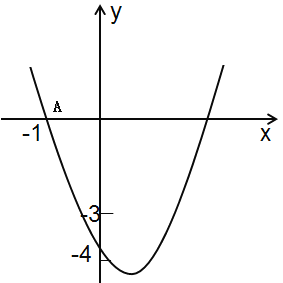
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),以下结论: ①
之间(包含端点),以下结论: ①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 没有实数根.其中正确的结论有( )
没有实数根.其中正确的结论有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
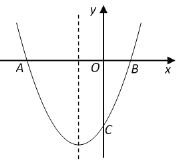
【题目】已知:抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 、
、![]() .
.
(1)求这条抛物线的函数表达式.
(2)在对称轴上是否存在一点![]() ,使得
,使得![]() 的周长最小.若存在请求出点
的周长最小.若存在请求出点![]() 的坐标.若不存在请说明理由.
的坐标.若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
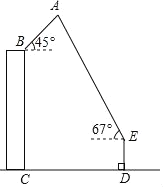
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
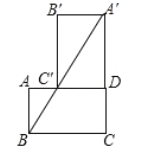
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 分别落在点
分别落在点![]() ,
,![]() ,
,![]() 处.
处.
(1)直接填空:当![]() 时,点
时,点![]() 所经过的路径的长为___________;
所经过的路径的长为___________;
(2)若点![]() ,
,![]() ,
,![]() 在同一直线上,求
在同一直线上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com