
【题目】如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.

(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
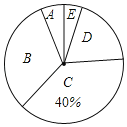
【题目】甘肃省注重建设“书香校园”.为了了解学生们的课外阅读情况,张老师调查了全班50名学生在一周内的课外阅读时间,并将统计的时间(单位:小时)分成5组:A.0.5≤x<1;B.1≤x<1.5;C.1.5≤x<2;D.2≤x<2.5;E.2.5≤x<3;并制成两幅不完整的统计图表如下:
组别 | 人数 | 占总数的百分比 |
A | 3 |
|
B |
|
|
C |
| 40% |
D | 9 |
|
E | 1 |
|
总计 | 50 | 100% |
请根据图表中提供的信息,解答下列问题:
(1)这次调查中学生课外阅读时间的中位数所在的组是 ;
(2)扇形统计图中,B组的圆心角为 ,并补全统计图表;
(3)请根据以上调查情况估计:全校1500名学生中有多少名学生每周阅读时间不低于2小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
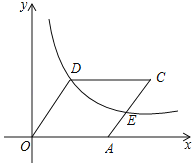
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
(k>0,x>0)的图象经过菱形OACD的顶点D和边AC的中点E,若菱形OACD的边长为3,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
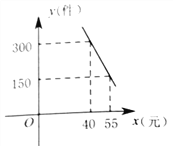
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
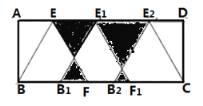
【题目】如图,在面积为![]() 的矩形
的矩形![]() 中作等边
中作等边![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 上,将
上,将![]() 向右平移得到
向右平移得到![]() (点
(点![]() 在
在![]() 的左侧), 再将
的左侧), 再将![]() ,
,![]() 向右平移,使
向右平移,使![]() 得与
得与![]() 重合,得到
重合,得到![]() (点
(点![]() 在
在![]() 的左侧),且第二次平移的距离是第一次平移距离的
的左侧),且第二次平移的距离是第一次平移距离的![]() 倍.若
倍.若![]() ,则阴影部分面积为_______
,则阴影部分面积为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙![]() 经过
经过![]() 两点,
两点,![]() ,点
,点![]() 是弧AB的中点,连接
是弧AB的中点,连接![]() 交弦
交弦![]() 于点
于点![]() ,
,![]() .
.
(1)求⊙![]() 的半径;
的半径;
(2)过点![]() 分别作
分别作![]() 的平行线,交于点
的平行线,交于点![]() 是⊙
是⊙![]() 上一点,连接
上一点,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,且
,且![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
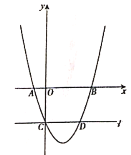
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该抛物线交于另一点
与该抛物线交于另一点![]() ,并且直线
,并且直线![]() 轴,点
轴,点![]() 为该抛物线上一个动点,点
为该抛物线上一个动点,点![]() 为直线
为直线![]() 上一个动点.
上一个动点.
(1)当![]() ,且
,且![]() 时,连接
时,连接![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是平行四边形
是平行四边形
(2)当![]() 时,连接
时,连接![]() ,线段
,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)连接![]() ,
,![]() ,试探究:是否存在点
,试探究:是否存在点![]() ,使得
,使得![]() 与
与![]() 互为余角?若存在,求出点
互为余角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com