
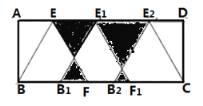
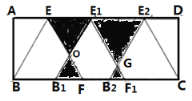
【题目】如图,在面积为![]() 的矩形
的矩形![]() 中作等边
中作等边![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 上,将
上,将![]() 向右平移得到
向右平移得到![]() (点
(点![]() 在
在![]() 的左侧), 再将
的左侧), 再将![]() ,
,![]() 向右平移,使
向右平移,使![]() 得与
得与![]() 重合,得到
重合,得到![]() (点
(点![]() 在
在![]() 的左侧),且第二次平移的距离是第一次平移距离的
的左侧),且第二次平移的距离是第一次平移距离的![]() 倍.若
倍.若![]() ,则阴影部分面积为_______
,则阴影部分面积为_______![]() .
.
【答案】![]()
【解析】
根据平移性质和矩形性质及勾股定理求出BE=BF=8,AE=DE2=4,EE2=AD-AE-BE2=12,EE1=![]() ,可求出S△BEF,根据相似三角形的判定和性质,由△BEF∽△EOE1,得
,可求出S△BEF,根据相似三角形的判定和性质,由△BEF∽△EOE1,得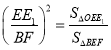 ,即
,即![]() .同理可得:
.同理可得:![]() ,
,![]() ,
,![]() .
.
因为四边形ABCD是矩形,△BEF是等边三角形
所以根据平移性质可得:AB=CD,∠D=∠A=90°,BE=CE2
所以∠ABE=30°,且△ABE≌△DCE2
所以BE=2AE,AE=DE2
设AE=a,则BE=BF=B2C=2a
所以AB=![]()
因为![]()
所以![]()
所以BC=BF+FB2+B2C=5a
所以由ABBC=80![]() ,得
,得
![]()
所以a=4
所以BE=BF=8,AE=DE2=4
所以S△BEF=![]() ,EE2=AD-AE-BE2=5a-a-a=3a=12
,EE2=AD-AE-BE2=5a-a-a=3a=12
因为E1E2=1.4EE1
所以EE1=![]()
所以E1E2=1.4EE1=7,B1F=8-3=3,B2F=8-7=1;
由已知可得∠OEE1=∠OE1E=60°,∠EBF=∠BFE=60°
所以△BEF∽△EOE1
所以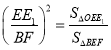
即![]()
所以![]() =
=![]()
同理,△BEF∽△FOB1
所以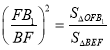
即![]()
所以![]() =
=![]() ;
;
同理,△BEF∽△E1GE2
所以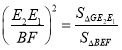
即![]()
所以![]() =
=![]()
同理,△BEF∽△B2GF2
所以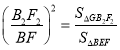
即![]()
所以![]() =
=![]()
所以阴影面积是:![]() +
+![]() +
+![]() +
+![]() =
=![]() +
+![]() +
+![]() +
+![]() =
=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,己知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,其对称轴与抛物线相交于点
,其对称轴与抛物线相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
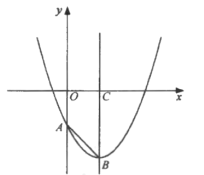
(1)求![]() 的长;
的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为![]() .若新抛物线经过原点
.若新抛物线经过原点![]() ,且
,且![]() ,求新抛物线对应的函数表达式.
,求新抛物线对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
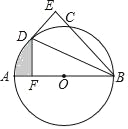
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,AD为弦,∠DBC=∠A.

(1)求证:BC是半圆O的切线;
(2)若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解我区居民知晓“创建文明城区”的情况,适合全面调查;
B.甲乙两人跳高成绩的方差分别为![]() ,说明乙的距离成绩比甲稳定;
,说明乙的距离成绩比甲稳定;
C.一组数据2,2,3,4的众数是2,中位数是2.5;
D.可能性是1%的事件在一次试验中一定不会发生.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年的寒假是“不同寻常”的一个假期.在这个超长假期里,某中学随机对本校部分同学进行“抗疫有我,在家可以这么做”的问卷调查:A扎实学习、B经典阅读、C分担劳动、D乐享健康,(每位同学只能选一个),并根据调查结果绘制如下两幅不完整的统计图.
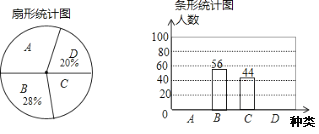
根据统计图提供信息,解答问题:
(1)本次一共调查了_______名同学;
(2)请补全条形统计图;在扇形统计图中A所对应的圆心角为 度;
(3)若该校共有1600名同学,请你估计选择A有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
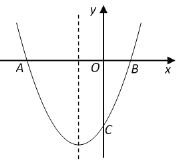
【题目】已知:抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() 、
、![]() .
.
(1)求这条抛物线的函数表达式.
(2)在对称轴上是否存在一点![]() ,使得
,使得![]() 的周长最小.若存在请求出点
的周长最小.若存在请求出点![]() 的坐标.若不存在请说明理由.
的坐标.若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.
(1)求今年6月份A型车每辆销售价多少元?(用列方程的方法解答)
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A、B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com