
【题目】如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )

A.  B.
B. 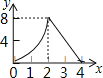
C. 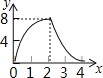 D.
D. 
【答案】D
【解析】
当0≤t≤2时,AM=t,AN=2t,利用S=S正方形ABCD﹣S△AMN﹣S△BCM﹣S△CDN可得到S=﹣t2+6t;当2<t≤4时,CN=8﹣2t,利用三角形面积公式可得S=﹣4t+16,于是可判断当0≤t≤2时,S关于t函数的图象为开口向上的抛物线的一部分,当2<t≤4时,S关于t函数的图象为一次函数图象的一部分,然后利用此特征对四个选项进行判断.
当0≤t≤2时,AM=t,AN=2t,
所以S=S正方形ABCD﹣S△AMN﹣S△BCM﹣S△CDN
=![]()
=﹣t2+6t;
当2<t≤4时,CN=8﹣2t,S=![]() (8﹣2t)×4=﹣4t+16,
(8﹣2t)×4=﹣4t+16,
即当0≤t≤2时,S关于t函数的图象为开口向下的抛物线的一部分,当2<t≤4时,S关于t函数的图象为一次函数图象的一部分.
故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
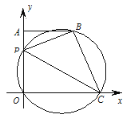
【题目】如图,在平面直角坐标系中,A(0,4),B(3,4),P 为线段 OA 上一动点,过 O,P,B 三点的圆交 x 轴正半轴于点 C,连结 AB, PC,BC,设 OP=m.
(1)求证:当 P 与 A 重合时,四边形 POCB 是矩形.
(2)连结 PB,求 tan∠BPC 的值.
(3)记该圆的圆心为 M,连结 OM,BM,当四边形 POMB 中有一组对边平行时,求所有满足条件的 m 的值.
(4)作点 O 关于 PC 的对称点O ,在点 P 的整个运动过程中,当点O 落在△APB 的内部 (含边界)时,请写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能热水器的玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最佳.如图,某户根据本地区冬至时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光与玻璃吸热管垂直).已知:支架CF=100 cm,CD=20 cm,FE⊥AD于E,若θ=37°,求EF的长.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
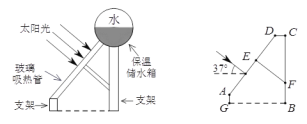
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=5,面积为20,∠BAD<90°,⊙O与边AB、AD都相切,AO=2,则⊙O的半径长等于( )
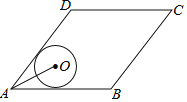
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
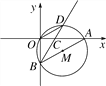
【题目】如图,在直角坐标系中,⊙M经过原点O(0,0),点A(![]() ,0)与点B(0,-
,0)与点B(0,-![]() ),点D在劣弧
),点D在劣弧![]() 上,连结BD交x轴于点C,且∠COD=∠CBO.
上,连结BD交x轴于点C,且∠COD=∠CBO.
(1)求⊙M的半径;
(2)求证:BD平分∠ABO;
(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;
(2)若菜园面积为384 m2,求x的值;
(3)求菜园的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
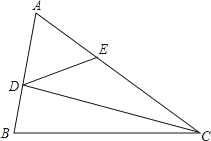
【题目】在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com